GEODEESIA 16.-17. sajandil  (Jaan Märss - viimati täiendatud 2010 a.)
1. Ristlatt
    navigatsiooni ristlatt
    kaugusmõõdik (ristlatt):
        kauguse mõõtmine ühe asukohaga
        kauguse mõõtmine kahe asukohaga
2. Mõõtelaud
    konstruktsioon
    kasutamine:
         tehniline varustus
         töö käik
         maamõõdu pikkusühikud
3. Nurgamõõdikud :
        kolmnurkmõõdikud
        kaaremõõdikud
4. Geodeesia maa-aluses sõjas






16. sajandi lõpul  leidsid   maamõõtmise  instrumendid  vaid sõjalist rakendust. Peale kindluste projekteerimise pakkus suurimat rakendust suurtükivägi.  Kuna proovilaskude tegemine oli kallis, siis oli kasulik teada sihtmärgi  kaugust, vastavalt tuli  leiutada kauguse mõõtmine ning vaenlase objektide plaanistamine. Juba 14. sajandil võeti kasutusele ristlatt, 16. sajandil lisandus mõõtelaud ja sajandi teisel poolel hulgaliselt erinevaid nurgamõõdikuid. 

Objektide kandmine kaartile e. topogeodeetiline sidumine :
- sks. k.   plotten,
-  ingl. k.  maping, 
- vene k.  засечка
- eesti k.  sälkimine (Suurtükiväeõpik 1996 ) tuleneb venekeelsest terminist 

Sks.-ingl. analoogia põhjal võiks eesti keeles kasutada sõna  "plaanistamine" või "kaardistamine" (kuigi eesmärgiks võis olla ka ainult kauguste mõõtmine). "Plaanistamine" sobib seejuures paremini, sest enamiku maamõõtmise instrumentidega  plaanistati ka vertikaalseid ristlõikeid (läbi kindlustuste vallide ja vallikraavide), mis ei kuulu otseselt kaardistamise valdkonda




1. Ristlatt  sks. jakobsstab, ka kreutzstab,  ingl. jacobstaff  -  tõenäoliselt juba antiikajal tuntud nurgamõõtmise instrument,  mis on keskaegses Euroopas esmakordselt kirjeldatud juudi  õpetlase ja  araabiakeelsete tekstide tõlkija  Levi ben Gerson´i poolt aastal 1342.
(Kuna ristlati abil ei mõõdeta nurka ega kaare pikkust,  vaid iseloomustatakse nurka juurdekonstrueeritud kolmnurga kaudu, siis kuulub ristlatt trigonomeetriliste e.  kolmnurkmõõdikute hulka.)

15. saj. on hakatud ristlatti kasutama  astronoomias (astrolaabi kõrval), samuti rannasõidulaevadel.

 -  miniatuurid aastast 1467  
URL: http://tarvos.imareal.oeawac.at/server/images/7002458.JPG        
Mastikorvis nähtav  viseerimisseadeldis võib olla ristlatt või selle modifikatsioon. Ristlatti on kasutatud rannalähedases meresõidus  selleks, et  püsida rannast ohutul kaugusel. Selleks on fikseeritud  rannal nähtavate  kinnispunktide vahelist nurka. (Samal otstarbel on lõigatud  pardasse viseerimiseks ka erinevaid märke.)               

Kauguse mõõtmiseks kasutatud ristlattidest on säilinud vaid üksikuid fragmente, veidi rohkem on kollektsioonides  säilinud meresõidul  navigeerimiseks kasutatud ristlatt-nurgamõõdiku detaile. (Kaugusmõõdik erineb nurgamõõdikust skaala jaotuste poolest: kaugusmõõdiku varre skaala  on lineaarne, nurgamõõdiku skaala - logaritmiline.) .     Vt. koondatud pildimaterjal




Navigatsiooni ristlatt  oli  nurgamõõdik, millega mõõdeti  merel taevakehade kõrgust. Kasutati kuni 18. sajandi keskpaigani, mil tõrjuti välja sekstandi poolt.  


1594
 http://www.photolib.noaa.gov/
htmls/theb2173.htm

URL: http://www.esys.org/
technik/jakobsstab.html
 16. sajandil võisid navigatsiooni ristlatid olla erineva ehitusega, 17. sajandil  kujunes neist välja  kindlakujuline instrument:
Vars (baculus) oli 2,5 jala pikkune, varre neljal küljel olid erinevad skaalad.
4 liikuvat ristpulka (cursor) olid vahetatavad : korraga võis latil olla vaid üks kursor - nurga  mõõtmiseks tuli valida võimalikult pikk kursor.  Igal kursori jaoks oli varre vastaval küljel oma  skaala.
Nurgamõõtmise käik:
Varre tömp ots toetatakse vastu põsesarna ja sihitakse  kursori alumise otsaga  silmapiiri, ülemise otsaga päikest või tähte. Kursorit nihutatakse varrel senikaua, kuni õnnestub viseerida mõlemat objekti üheaegselt - seejärel võetakse varre skaalalt lugem (kraadides).




Ristlatt-kaugusmõõdik  on instrument, millega mõõtmisel kasutatakse kolmnurkade sarnasust.  Ristlati elemendid (vars ja kursor) moodustavad  nihutamisel võrdluskolmnurga,  mis võimaldab arvutada kaugust kas pika ja lühikese külje suhte või  eelnevalt kindlaks tehtud mastaabi  järgi  (vastavalt meetod "ühe asukohaga" või "kahe asukohaga")

Tänapäeva armeebinokliga kauguse mõõtmine toimub "ühe asukohaga", kasutades sarnaste kolmnurkade külgede suhet (proportsiooni), mis on binokli seesmise konstruktsiooni kaudu fikseeritud:  -  binokli vaateväljas on niitristik, mille kõige väiksem jaotis (NMJ) moodustab vaataja silma suunas teravatipulise  kolmnurga pikendusega 1:1000 (kolmnurga pikad haarad võime seejuures lugeda praktiliselt võrdseks)   
  - NMJ projektsioon viseeritaval objektil ja objekti kaugus  moodustavad eelmisele sarnase pikendatud kolmnurga, mille haarade pikkus (objekti kaugus) on 1000 korda suurem kui 1 NMJ  projektsioon objektil
 -kui viseerija suudab kalkuleerida, kui pikk (mitu meetrit) on  ühele jaotisele vastav pikkus objektil või selle läheduses (viseeritakse teadaoleva pikkusega objekte, nagu inimesed, sõidukid, telefonipostid, postide vahed, majakorruste kõrgus jms.), siis  tarvitseb kauguse leidmiseks korrutada see kalkuleeritud pikkus vaid  tuhandega.
(Käibekeeles nimetatakse seepärast binokli skaala vähimaid jaotisi "tuhandikeks", mis pole sisuliselt siiski õige.  Armeebinokli jaotiste pikkus on valitud spetsiaalselt  peast arvutamiseks nii, et   ringjoone kaar on jagatud 6000-6400 nurgamõõdu jaotiseks (NMJ) - NATO-riikides 6400, Rootsis 6300, Venemaal ja Soomes 6000 NMJ - mis annab optikasse sisseehitatud mõõtekolmnurga aluse ja kõrguse suhteks ca tuhat.  Suurtükiväeõpik - Peets & Tiidolepp)
   
Ristlati puhul võiks kasutada samasugust varda ja kursori pikkuste fikseeritud suhet  - tollsüsteemi puhul näiteks vähima tollijaotise (enamasti 1/8-tolli) ja ühe jala pikkuse suhet, mis on 1:96 -  kuid tollsüsteemis arvutamist ei teinud see kindlasti lihtsamaks. Tähtsam oli ilmselt see, et  kursori-varreskaala suhet viseerimisel muutes saadi ristlatile lõpptulemusena kindlad näidud, mida võis hiljem rahulikult lugeda ning teostada vajalikud arvutused.  (Ristlati puhul võisid viseerimise ja arvutamisega tegeleda ka erinevad isikud, mis pole tänapäeva armeebinokliga võimalik.)

Sõltuvalt ristlati tüübist võis mõõteriista võrdluskolmnurga suhet muudeti   kolmel erineval viisil.


Kursorit nihutatakse latil
Kursorit nihutatakse
läbi lati ava
Latti pikendatakse teleskoobina



Kauguse mõõtmine  ühe asukohaga("mit einem Stand"):  peale objekti kahe kinnispunkti viseerimist saadakse ristlatile võrdluskolmnurk, mille moodustavad vaatleja silm ning kursori kaks otspunkti. Selle võrdluskolmnurga külgede mõttelisel pikendamisel objekti kinnispunktideni saame sarnase kolmnurga, mille külgedel on sama proportsioon. Kui oleme kalkuleerinud kinnispunktide vahelise kauguse ja jaganud selle kursori pikkusega, saame teada kolmnurga mastaabi, mastaabi korrutamine mõõteriista varre skaalanäiduga annabki meile lõpptulemusena kauguse.
Tollsüsteemi ühikute korrutamine ja jagamine tuli ilmselt teostada paberil. 16.-17. sajandil  sooritati tehteid paberil juba araabia numbritega ning samasuguste paigutamise juhendi (algoritmi)  järgi  nagu tänapäeval, ainus erinevus võis olla vahejoonte tõmbamises, mida õpetajad nõudsid erinevalt. 
(Vt. araabia numbritega (numbrilise e. digitaalse) arvutamise näide aastast 1624 ,  paralleelselt kasutati küll üle 400 aasta ka arvutamist hulkadele vastavate  nuppudega (analoogarvutamine), mille nimetuseks oli 15.-18. sajandini  "joontel arvutamine".
Joontel arvutamise lõpptulemus võidi veel 17. sajandil kirja panna ka rooma numbritegal. Joontel arvutamise viimaseks näiteks on  veel 20. sajandil kasutusel olnud arvelaud. )   URL:http://www.bbf.dipf.de/VirtuellesBildarchiv/

Kui  tänapäeva  armeebinokli mõõtekolmnurga proportsioon (aluse ja kõrguse suhe) on 1:1000,  siis  ristlati  kursori ja lati pikkuste suhe, mida näeme ajastu gravüüridel,  vajab  visuaalset ümbertõlgendamist :
 -  gravüür ei saa  kujutada proportsionaalselt õiget distantsi,  mis on tegelikkuses kümneid kordi pikem
 -  et viseerimist õigesti kujutada, on suurendatud vastavalt ka viseerimisnurka
 -  vastavalt viseerimisnurga suurendamisele on joonistel suurendatud oluliselt  kursori pikkust
JÄRELDUS:  võrreldes piltidel kujutatuga on kursorid olnud tegelikkuses kümneid kordi lühemad! 

Toodud tõlgenduse tõestuseks näeme  gravüüridel viseerimiseks valitud - ilmselt siis sobivaid - objekte, sealhulgas ka tornide avasid, mille vähene kõrgus nõuab viseerimiseks eriti lühikest kursorit (400 m kauguselt  2 m laskeava viseerides pidi 4 jala (ca 120cm) pikkuse skaalaga  latil olema kahe 1/8" pikkune (ca 6-7 mm) kursor). 
MÄRKUS:  nii lühike kursor suurendas oluliselt mõõtmisviga, samas kui kauguse mõõtmisel "kahe asukohaga" (vt. allpool) võis kursor olla tunduvalt pikem, mis andis ka suurema täpsuse.



URL: http://www.mhs.ox.ac.uk/
measurer/text/mathemat.htm		 - kaugusmõõdik 16. sajandist (pikkus 3 jalga)                                                    
Kui laskeva kõrgus oli umbes inimese mõõtu, siis pidi  400 meetri kauguselt viseerimiseks olema varre ja kursori pikkuste suhe  üle 1:200. Pildil oleval instrumendil võis kursori pikkus olla  sobiv.

VÕRDLUSEKS: Rannakaitses võis viseerida ja kalkuleerida sõjalaeva mastide kõrgust. Kui viseerime laeva jõudmist tema suurtükkide laskekaugusele (ca 600 m) ja teame seejuures, et mastide kõrgus on  30-35 m, siis saame kolmnurga pikenduseks 1:20. Ühe meetri pikkuse lati korral pidi kursori pikkus olema seega  5 cm . (Võrdle ka:  Daumensprung )  






Kauguse mõõtmine kahe asukohaga  on ajastu gravüüridel kõige levinum  (vt. Wikimedia_2010)

Viseerimisel võib valida teineteisest tunduvalt kaugemal asetsevad kinnispunktid. Kalkuleerimist ei toimu, selle asemel määratakse sarnaste kolmnurkade mastaap - meetodil, mida tänapäeval ei kasutata. Kui mastaap teada, korrutatakse see  ristlati varre skaalalt loetava pikkusnäiduga.



                                                                                                               
  - mastaabi määramise selgitus (http://hdl.loc.gov/loc.rbc/rosenwald.1363)                                                       
1) esimene asukoht
   - leitakse sobiv vaatesiht ning valitakse viseerimispunkt
   - viseeritakse  kaht objektil nähtavat kinnispunkti
2) teine asukoht
   - eemaldutakse objektist täpselt mõõdetud vahemaa võrra
   - viseeritakse samu kinnispunkte uuesti 
3) fikseeritakse lati skaalal näitude vahe
4) arvutatakse mastaap (asukohtade vahemaa jagatakse näitude vahega)
     


                   

        www.bbf.dipf.de/VirtuellesBildarchiv/ 
     

    Kahe asukohaga viseerimine oli kindlasti täpsem kui ühe asukohaga meetod:
-  puudus silma järgi kalkuleerimise viga, mida suurenes paljukordselt korrutamisel proportsiooniga
-  suurem viseerimisnurk (pikem kursor) andis  suurema täpsuse (navigatsiooni ristlatil kasutati täpsuse            suurendamiseks  võimalikult pikki,  vahetatavaid kursoreid)

Kõige täpsem kauguse mõõtmine toimus mõõtelaua ja nurgamõõdikuteabil vastase objekte plaanistades (teadaoleva pikkusega kolmnurga külg võis olla sadu kordi pikem ning  väga täpselt mõõdetud)  Samas oli  ristlatiga võimalik mõõta kaugust vaid ühe vaatesihi kaudu,  mõõtelaua ja nurgamõõdikute puhul pidi vaatesihte olema kokku isegi kolm.
                                                                                                                                     tagasi sisukorda









2. Mõõtelaud  (lad. mensula, sks. messtisch, ingl. plane table, soome k. mittauspöytä)
Eestikeelses terminoloogias (Tehnikaleksikoni järgi)  on kasutusel nimetused mensul (lad. mensula - "lauake")
ja plaanistamislaud.
    Seoses põllumajandusliku mõõdistamisega on eestikeelne "plaanistamine" küll sobiv,  kuid sõjanduses  on sama töövahendit kasutatud ka lihtsalt kauguste mõõtmiseks, ilma plaanistamiseta. Sõjanduslikus kasutuses tuleks universaalsemaks  pidada saksa- ja soomekeelset nimetust, mille otsetõlge oleks  "mõõtelaud".

Esimesed täies varustuses mõõtelaua kirjeldused pärinevad Prantsusmaalt (1551  Abel Foullon, Paris, 1591  Digge ), kuid joonised puuduvad.  Kuna 1551.a. kirjeldati juba täielikult varustatud mõõtelauda, siis pidi  instrument olema veel tunduvalt vanem.
    17. sajandi algusest pärineb juba  jooniseid, mille järgi on tänapäeval tehtud rekonstruktsioone. Jooniste tõlgendamist raskendab asjaolu,  et  autorid kirjeldavad enamasti  omapoolseid täiustusi algsele mõõtelauale, mida me ei tunne, seetõttu leiavad  kirjeldamist suhteliselt  ebatüüpilised konstruktsioonid.

Mõõtelaua levikut  soodustas selle  kasutamise lihtsus -  vaja oli mõõta vaid  üksikuid lõike maastikul (mõõteketi-, -nööri või -latiga), samas polnud vaja teostada nurkade mõõtmisi ega trigonomeetrilisi teisendusi (nurgaväärtustelt külgede suhtele ja vastupidi). Arvutusi mastaapide teisendamisel võib pidada erandjuhtumiks.

Rootsi Kuningriigis algasid  1628.a. maakasutusega seotud plaanistamistööd ning algas ka maamõõtjate koolitamine  (peamiselt Uppsala ülikooli baasil). Peale Tartu ülikooli asutamist 1632.aastal alustati maamõõtjate ettevalmistamist ka kohapeal. 1665. aastal on Tartu Ülikooli matemaatikaprofessor Joachim Schelen avaldanud raamatu Cursus mathematici, mille IV peatükk on pühendatud geodeesiale. Kui Eesti alal algasid algasid 1681.a. Rootsi Suure Katastri  mõõdistustööd, siis oli suurem osa Eesti alal tegutsenud maamõõtjatest siiski Uppsala haridusega. (Kalev Koppel 2005)
 ( Magistritöö URL: http://dspace.utlib.ee/dspace/bitstream/10062/1263/5/koppelkalev.pdf )





Mõõtelaua ehitus
Järgnevalt  tuntumad autorid, kellelt praktilise geomeetria käsiraamatutes leidub peatükke mõõtelauast.


Johann Richter alias Johannes Praetorius (1537-1616) - mõõtelaua kirjeldus aastast 1610 (1590?),
algupärast joonist pole teada.
                                                                                                                                           
  nn.  "Pretoriuse mõõtelaua" joonis aastast 1627 (Richteri õpilase Daniel Schwenteri käsiraamatust, antud koopia pärineb Andreas Böckleri poolt välja antud  kompilatsioonist a. 1667.)

Pretoriuse mõõtelauda peeti juba tema kaasaegsete poolt klassikaliseks, ilmselt järgis see varasemate (prantsuse?) mõõtelaudade lihtsamat ehitust. Võrreldes Zubleri ja Kircheri laudadega puudub pöörlev välisraam, sihikud paiknevad otse joonlaual (alidaad). Sellisel kujul on "Pretoriuse mõõtelaud" kujunenud mõõtelaua üldnimetuseks, mida on kasutatud kuni 1920-ndate aastateni.        
Schwenteri-Pretoriuse mõõtelaua eripäraks on  kolmnurkmõõdikuna toimiv kaldenurga mõõdik laua seval, mida teistel mõõtelaudadel ei esine. Kaldenurga mõõdik võimaldas konstrueerida vertikaalseid läbilõikeid - näiteks läbi vallide ja vallikraavi  - mis oli mullatööde puhul väga oluline).
   Pilt aastast 1670 -
 - URL: http://commons.wikimedia.org/wiki/Category:Old_Manuscripts_from_the_Deutsche_Fotothek

Vt. väljavõte 1667.a. käsiraamatust (valmistamise kirjeldus)                                                              Flash Schwenteri-Pretoriuse mõõtelauast (Suomen Virtuaaliyliopisto - detailide nimetused on       soome keeles).  
Vt. rekonstruktsioon -  Soome Maamõõtmisvalitsuse Muuseumis on Pretoriuse mõõtelauast                valmistatud  lihtsustatud rekonstruktsioon.                                                                                           
                                                                                                                                                                  tagasi sisukorda


Leonhard Zubler (1563-1609) - mõõtelaua kirjeldus aastast 1607,  pilt aastast 1625

Zubleri  mõõtelaua keskel on kettakujuline laud, millele asetatakse kaart, kettale on kinnitatud ka kompass.  Joonlauda saab nihutada rööbiti nii, et see jääb sihtimisjoone suhtes paralleelseks. Sihikud ei paikne joonlaual, vaid välisraami küljes (pildil selle ülaosas), mida saab sihtimisel pöörata, . 
    Keerukuse poolest on Zubleri mõõtelaud võrreldav hilisema  Kircheri mõõtelauaga, erinevus on vaid sihiku tüübis. (Kumbki mõõtelaud  ei leidnud hilisematel sajanditel kasutust, samas on autorite käsiraamatud säilinud ja leiavad palju tähelepanu..)

        
                                                                                                                                                    
Athanasius Kircher (1602-1680) - mõõtelaua kirjeldus 1643, joonised tema õpilaselt (Kaspar Schott 1660) .

Vt.  Das Pantometrum Kircherianum – Athanasius  Kirchers Messtisch  In: Beinlich, H., H.-J. Vollrath, K. Wittstadt (Hrsg.), Spurensuche – Wege zu Athanasius  Kircher, Dettelbach (Röll) 2002, 119-136

Kircheri mõõtelaud "Pantometrum" sarnaneb väga Zubleri mõõtelauaga, erinevus on vaid sihiku tüübis. Kuna sihtida tuleb ka laua tasapinnast kõrgemal või madalamal paiknevaid märke, siis on Kircher paigutanud laua servale astronoomiast tuntud astrolaabi tüüpi sihiku (alidaadi)
  
Pildid salvestatud:  http://www.google.co.uk/books.........                           


   
Daniel Schwenter & Andreas Böckler  - mõõtelaua kirjeldus praktilise geomeetria käsiraamatust 1667.

   "...Suurem laud, laiuseks kõige mugavam võtta poolteist jalga, sellele mahub küllaltki suur paber, ka võib sinna peale töö lõpetamist asetada hea joogi ja tüki leiba..."  

 Vt. väljavõte 1667.a. käsiraamatust (valmistamise kirjeldus). Kolmjala eripäraks on tüve sisse pöörduvad jalad, samuti alt kalasabatapiga kinnituv lauatahvel                                                   

                                                                                                                                                                 tagasi sisukorda      


Mõõtelaud itaaliakeelsest  visandite raamatust (USA Kongressi Rmtkg Rosenwaldi kollektsioonis kannab nimetust  "Sketchbook of Military Art")  -  17. sajandi esimene pool? -  Vt.  bibliograafiline informatsioon )  
Digitaliseeritud kujul vt.   lehekülje valikuga ,  PDF (102,25 MB)

TÕLGENDAMIST vajab antud visandiraamatu ja praktilise geomeetria käsiraamatute võrdlus:  kogu visandiraamatu sisust on näha, et see taotleb pigem tutvustamist kui  vajadust esitada oma leiutisi ja fantaasiat. Samal ajal kui hinnaliste trükiste-käsiraamatute autorid on  taotlenud sageli  maksimaalset  keerukust ja  uuendusi  (et tõestada  rahastajale  oma kompetentsust), siis võib odavas visandiraamatus  kujutatu olla oma  ajastule küllalti tüüpiline.
 
   Võrreldes eelmise nn. "mugava"  kolmjalaga (Schwenter&Böckler) on konstruktsioon praktiline (puudub fantaasiaküllaste liialdustega  tappimistöö). Lisaks kolmjalale ja tahvlile on kujutatud veel kaht joonlauda, millel on figuraalsed, samas aga lihtsa sihtimisservaga sihikud.Kõrget mõõteskaalaga sihikut (nagu Pretoriuse mõõtelaual), mis  oleks võimaldanud sihtida laua tasapinnast üles- või allapoole ning mõõta kaldenurki,  antud mõõtelaual pole.   
      http://hdl.loc.gov/loc.rbc/
      rosenwald.1363

VÕRDLUSEKS PIKEMALT  (kuna Ingeri bastioni käikudes on antud mõõtelaua rekonstruktsioon,  lisatud on vaid kaldenurga mõõdik Pretorius&Schwenteri mõõtelaualt):
1) Visandite raamatus on joonlaudadel  figuraalsed sihikud, mille üks serv on sihtimiseks sirge.  
    Fantaasiarikkad käsiraamatud esitlevad küll tunduvalt keerukamaid sihikuid, neid  näeme ka eksklusiivsetel  täismetallist                      nurgamõõdikutel, kuid sõjaolukorras võis lihtne sihik olla kasulikum. Viseerijal tuli töötada  võibolla  hämaras, ka  polnud tal               vaenlase territooriumile  võimalik paigutada värvilist lipukest. (18.-19.sajandi maamõõtja töötingimused olid teistsugused.)
       
   Michael Coignet´  nurgamõõtja-bussool 17. saj. algusest,                  
    millel on  sirge servaga  sihik ja  kokkupandavad jalad 
     URL: http://www.mhs.ox.ac.uk/measurer/text/mathemat.htm

2) Pretorius&Schwenteri kolmjalal on täispikkuses jalad,  samas kui visandiraamatu kolmjalg koosneb tüvisest ja  lühematest jalgadest, mis kokku pöörates annavad  lühema paketi. (Pikema tüvise ja lühikeste jalgadega konstruktsioonid  on  17.saj. piltidel kõige enam levinud.)
 
3) Pretorius&Schwenteri kolmjalg on stabiilne vastavalt sellele,  kui tugevasti on  kinni  pingutatud liblikmutrid. Visandiraamatu  kolmjalal on  seevastu "iselukustuvad jalad", mis  pöörduvad ja fikseeruvad  ise 45°all            (liblikmutrid on vaid stabiliseerimiseks). Selline konstruktsioon võis olla mugav sõjaolukorras ning ratsa             liikudes, samas kui maamõõtja võis täispikkade  jalgadega (nn. pretooriuse  mõõtelaua) võtta lihtsalt õlale.
 
(Sellisel kujul muutus nn. "pretoriuse laud"  18.-19. sajandi  rootsi maamõõtja tüüpiliseks töövahendiks - ka Eesti aladel.)

 1697
 1735
 1698		 - maamõõtjaid  Rootsi rahvusatlasest      
http://web.telia.com/%7Eu88707288/index.htm
/äldre_geodetiska_instrument_mus60
- salvestatud 2009.a.
  





Georg Conrad Stahl - mõõtelaua ning  joonlauasihikute jooniseid aastast 1687. Palju tähelepanu on pööratud  sihikute täiustamisele, et sihik ei  varjaks viseeritavat märki.  

            
 URL: http://commons.wikimedia.org/wiki/Category:Old_Manuscripts_from_the_Deutsche_Fotothek
 
                                                                                                                                    
                                                                                                                                                                            tagasi sisukorda





Mõõtelaua kasutamine.  
Vt. pildimaterjal,  sama - keritaval kujul

Tehniline varustus.
Vaatamata erisustele jäi  17. sajandil domineerima kõige lihtasam e. nn. pretoriuse mõõtelaud(mensul, plaanistamislaud). See koosnes kolmjalast ja selle peale kinnitatud pöörlevast lauakesest. Laua peal kasutamiseks pidid komplekti  kuuluma viseerimisjoonlaud (alidaad), mis oli varustatud sihikuga (diopter), pikkuste ülekandmiseks oli torke- e.  mõõtesirklit, joonte tõmbamiseks oli  teraspliiats.  
    Joonte edasikandmiseks on kasutatud paralleeljoonlauda, plaanide-kaartide teisendamisel on kasutatud   proportsionaalsirklit ja pantograafi  (ei kuulunud välitööde varustuse hulka - vt. abivahendid)
    Joonlaua peale oli graveeritud mastaapskaala: lihtskaala oli valmistatud kõvemast lehtpuust (pirn), transversaalskaala graveeriti messingist joonlauale 

Transversaalskaala  e. kaldjoontega  mastaabiskaala oli plaani või kaarti koostaja  töövahend, mis võimaldas sellist täpsust, nagu  oleks tänapäevane jaotis - millimeeter - jagatud  veel viieks  ( 1/64 tolli = 0,4 mm, mille võis silma järgi jagada veel pooleks).  Valmis kaartile kanti harilikult  lihtskaala.

    arv:   1775                 
Mõõtesirkliga lugemi võtmine:
1) sirkli  haarad asetatakse skaala välisservale nii, et jääk  satuks kaldjoonte (transversaalide) jaotusse, teise haara ristjoonelt  võetakse osaline lugem
2) transversaalide jaotuse välisservalt võetakse järgmine osalugem
3) sirkli mõlemad haarad nihutatakse rööbiti alla kuni teravik lõikub transversaaliga - ning võetakse skaala otsalt viimane osalugem


Paberiks on olnud  kaltsupaber, kvaliteedilt ja suuruselt  regalpapper, regalark , mis mahtus mõõtelauale suurusega  13 x 17 tolli. (Heikki Rantatupa 2008  - http://www.vanhakartta.fi/)
Paberi kinnitamiseks lauale kasutati terasnaelu, mille sisselöömiseks ja väljatõmbamiseks võis olla spetsiaalne sõraga haamrike.
    Mõõtelaua horisontaalseks rihtimiseks  kasutati  nurgikuga ripploodi. 
    Ilmakaarte järgi oreinteerimiseks pidi laual  olema  kompass. Kompassi järgi orienteeriti mõõtelaud põhja-lõunasuunaliseks ning tõmmati  paberile kompassi nõela suunda tähistav joon. Hiljem tuli selle järgi  joonistada  kaardile  kompassiroos, mis võimaldas  kasutajal kaardi  õigesti suunata.

Rootsi Kuningriigis anti 1636.a. välja instruktsioon selle kohta, milliseid tingmärke kaartidel kasutada ja kuidas kaarte värvida. Kompassiroos muudeti kohustuslikuks, kuid ilma täpsema juhendita, mis võimaldas igal  maamõõtjal joonistada  endale isikupärase kompassiroosi.

Vt. Soome alal tegutsenud rootsi maamõõtjate kompassiroose 17. saj. 18. saj. algusest  
Suomen Virtuaaliyliopisto http://palvelut.virtuaaliyliopisto.fi/maakirjakartat/historia/kompassiruusut.html


Allmaatöödel võis mõõtelauda kasutada  ka bussoolina.  Kui plaanile oli tõmmatud põhi-lõuna suunda tähistav joon, siis pöörati ka  maa all  plaani nii, et  kompassi nõel osutaks samas sihis. Seejärel viseeriti joonlauaga käigu suund ning tõmmati plaanile joon.  Sisuliselt fikseeriti nii kompassi nõela ja viseerimissuuna  vaheline nurk, mis on bussooli tunnus.


 Viseerimispunktide vahe mõõtmiseks maastikul  pidi komplektis olema 25 küünra pikkune rauast maamõõdukett, mille otstes olid vasest kinnitusrõngad ja kaks 5 jala pikkust maamõõduvaia keti pingutamiseks.
Teise viseerimispunkti ("jaama") tähistamiseks  oli  vaja püstitada liiniteivas. http://www.bbf.dipf.de/VirtuellesBildarchiv/

                                                                                                                                                                        tagasi sisukorda

 



Töö käik.
Viseerimisjoonlaua ja pliiatsi abil  konstrueeriti  paberile kindlas mastaabis kolmnurgad, mis moodustasid plaanil või kaardil võrgustiku (graafiline trianguleerimine). Arvutused ega trigonomeetria tundmine polnud vajalikud.

- mensulmõõdistamine Palvere mõisas 1690. aastatel (Kalev Koppel 2008)


Kolmnurga konstrueerimine mõõtelaual e. graafiline trianguleerimine.

 Mõõtelaud tuleb üles seada järgemööda kahes viseerimispunktis e. "jaamas". Selleks leitakse  maastikul  punktid,  kust  objekt (näiteks bastioni nurk) oleks sihitav e. viseeritav,  viseeritavad peavad olema  punktid ka omavahel.
- klikkimisel avanev pildimaterjal :
   http://www.bbf.dipf.de/VirtuellesBildarchiv/
   http://commons.wikimedia.org/wiki/Category:Old_Manuscripts_from_the_Deutsche_Fotothek


1) Mõõtelaud seatakse üles ühte punkti, teise punkti seatakse üles tähis - hästi nähtav värviline latt või lipuke.
2) Mõõtelauale kinnitatakse paber, selle vaenlasest kaugemale servale  asetatakse sihikuga viseerimisjoonlaud, sihitakse teise viseerimispunkti suunas ning tõmmatakse paberile joon (baasjoon).
3) Viseerimispunktide vahe mõõdetakse mõõteköie, -keti või -latiga.
4) Vastavalt mastaapskaalaga joonlaualt leitakse mõõdetud vahemaale vastav lõik, võetakse mõõtesirkli teravike vahele ja kantakse üle baasjoonele - sellest saab tulevase kolmnurga alus.
5) Teise või sama viseerimisjoonlauaga  viseeritakse nüüd  sirglõigu  ühest otsapunktist vaenlase objekti suunas ja tõmmatakse paberile teine joon - jooned moodustavad nurga.
6) Mõõtelaud viiakse üle  teise viseerimispunkti, seal olnud tähis tuuakse esimesse (toimub vahetus).
7) Mõõtelaud seatakse uues kohas horisontaalseks, viseerimisjoonlaud asetatakse baasjoonele ja sihitakse lauda pöörates, kuni suund on täpselt lipukesele eelmises viseerimispunktis - kolmnurga alus on jälle õiges sihis.
8) Nüüd viseeritakse joonlauaga aluse teisest punktist  vaenlase objekti suunas, tõmmatakse joon - ning kui vaenlase suunas tõmmatud jooned paberil ristuvad, on kolmnurk valmis.(Kui jooned laual ei ristu, tuleb valida teistsuguse  mastaabiga skaala või vähendada viseerimispunktide vahekaugust - tundmatu kauguse mõõtmisel käib see katseliselt.)
9) Kolmnurga tipu (vaenlase bastioni nurga) kaugus kolmnurga alusest võetakse mõõtesirkli  teravike vahele ja loetakse mastaapskaalalt selle tegelik kaugus maastikul.
 



MÄRKUS:  Rootsi Kuningriigis ja provintsides on ühikud sõltunud kasutusvaldkonnast:

Linnaplaanidel on pikkusühikuks Renlandsche Rod (Valdeko Vende - "reini latt", Peeter Tarvas - "reini vits")   - lüh. RR  (= 12 reini jalga =3,766 m )
Ehitusplaanidel on pikkusühikuks jalg  (laevajoonistel  esineb sageli  mastaapskaala, kus on samaaegselt inglise, prantsuse ja rootsi jalg).
Maakatastri plaanidel on pikkusühikuks  aln (küünar), mille pikkuseks on 2 rootsi jalga (2 x 0,279 m = 0,558 m)
Vt.täpsemalt  mensulmõõdistamine   :
(Kalev Kopppel:  URL=http://web.archive.org/web/20070612052010/
http://dspace.utlib.ee/dspace/bitstream/10062/1263/5/koppelkalev.pdf )

Mõõtelaua võrdlus nurgamõõdikutega:
  -  mõõtelaua abil kaugust mõõtes polnud vaja näitusid üles kirjutada ega neid hiljem paberile üle kanda - seega      polnud vaja ka  vastavaid abivahendeid. 
  -  sõltuvalt viseerimisjoonlaudade pikkusest võis mõõtmistulemus olla ka täpsem

                                                                                                                                    tagasi sisukorda




3. Nurgamõõdikud
URL:http://www.mhs.ox.ac.uk/geometry/
URL:http://www.mhs.ox.ac.uk/epact/
Nurgamõõdikuid  maamõõtmisel  ei kasutatud,  neid hakati rakendama  alles triangulatsioonivõrgustike loomisel 18.-19. sajandil (muud tsiviilrakendused olid veel  astronoomia, navigatsioon ja allmatööd).
Mõõtelauaga võrreldes oli nurgamõõdiku  kasutamine  keerulisem, kuna  nõudis nurgaväärtuse fikseerimist, hiljem nende ülekandmist kaardile.
 
Nurganäitude ülekandmiseks  paberile  leiutati  joonestamise abivahend -     
-  nurgamall
sks. k. transporteur
pr. k. rapporteur
ingl. k. protractor                                                          




Trigonomeetrilised- e. kolmnurkmõõdikud   on instrumendid, mis iseloomustavad nurka täisnurkse kolmnurga külgede suhte kaudu (nurga haaradele konstrueeritakse juurde kolmas külg, mis tekitab täisnurkse kolmnurga).
    Kolmnurga külgede suhet fikseerides nurga väärtust kraadides enamasti ei fikseeritud. Trigonomeetrilise suhte  nimetuseks oli 16.-17. sajandil  enamasti "proportsioon".

MÄRKUS: kolmnurkmõõdikute hulka kuulub ka ristlatt   (kirjeldatud ülal  p.1).

Kolmnurkmõõdikud koosnesid sirgetest elementides, milleks võisid tõenäoselt olla ka puust valmistatud joonlauad-liistud. Kolmnurkmõõdikute elementide suurem pikkus neile kaareskaalaga instrumentide kõrval  ilmselt ka suurema täpsuse -  kuni 18. sajandi keskpaigani, mil metallist kaaremõõdikute  skaalasid hakati graveerima ja sageli ka lugema luubi abil (näit. sekstandid).  vt. album

Kollektsioonides on proportsioonitult palju säilinud eksklusiivseid värvilisest metallist  instrumente, samal ajal kui teadaolevaid puidust instrumente - mõõtelaudu ja ristlatte - pole tänapäevani säilinud (on ainult fragmente).


1667
1687		 - kolmnurkmõõdikud  koosnesid sirgetest elementidest, millele olid asetatud sihikud.

                
 
 
- trigonomeetriliste funktsioonide nimetused olid 17. sajandil juba samad mis tänapäeval. Trigonomeetrilise suhte teisendamiseks olid kasutada  4-kohalised trigonomeetrilised tabelid.


1641  


Trigonomeetriline teisendamine  (suhtelt nurgale ja vastupidi) toimus välioludes  mitte tabeli, vaid  kvadrandi abil, millel oli lisaskaala.  Kvadrandi   90-kraadise kaare sisse oli paigutatud nelinurk, mille külje pikkuseks oli tollmõõdustiku aegadel "ümmargune" arv e. 1 jalg. Üks jalg jagunes 12 tolliks, see omakorda kokku 96-ks kaheksandiktolliks,  lugemi võtmiseks pingutati lihtsalt kvadrandi ripploodi nööri.
1/8" on ca 1,6 mm, mis oli enamasti tollskaalade kõige peenem jaotis, tunduvalt täpsema tulemuse saamiseks kasutati transversaalskaalat. 


1547
17. sajand		  - trigonomeetrilise teisendamise kvadrant olid 90-kraadise skaalaga kaaremõõdik, mille kaare sisse oli konstrueeritud kolmnurkskaala (kolmnurk moodustati  kvadrandi ripploodi abil)


URL: http://commons.wikimedia.org/wiki/
Category:Old_Manuscripts_from_the_Deutsche_Fotothek.  

- ühendatud kaare- ja kolmnurkmõõdik

Teisendamine oli vajalik kolmnurkmõõdikute ja kaaremõõdikute näitude võrdlemisks, mida tuli kõige enam  ette suurtükkide sihtimisel:
a) suurtüki 9o-kraadine kvadrant oli kaaremõõdik,
b) suurtüki vertikaalne sihik oli  kolmnurkmõõdik


Kolmnurkmõõdiku arhailine põhimõte on jätkuvalt kasutusel  ka tänapäeval - valdkondades, kus on tähtis peast arvutamise ja tulemuste tajumise  kiirus.
Armeebinoklitel ja optiliste teodoliitide  kaugusmõõdikutel on  optikasse sisseehitatud sirgetest elementidest kolmnurk, mis annab  kauguse (kolmnurga pikema külje) ja vaateväljas nähtava niitristiku vähima jaotise (kolmnurga lühema külje)  suhteks 1:1000. (Kolmnurga kaht pikemat külge pole vaja kaugusmõõtmisel eristada, kuna see  annab väga väikese vea:  "väikeste nurkade siinused ja tangensid on praktiliselt võrdsed"). Kui objekti sihtides õnnestub õigesti kalkuleerida niitristiku jaotisele vastava osa pikkus, tuleb see kauguse saamiseks orrutada tuhandega  (Teodoliidi pikksilmaga viseeritakse ja loetakse sihtlatil olevat meeterskaalat.) 

Maantee kaldenurka  iseloomustatakse protsentides, mis on inimese tajumisvõimele kohasem kui kraadides väljendatud nurk.  Liiklusmärkidel olev tee kaldenurk e. gradient 8%  tähendab näiteks, et 100 m kohta on tõus/langus 8 m. (Tollsüsteemis vastab protsendile suhe mitte saja, vaid üheksakümnekuue osa suhtes.)  
-detsimaalsüsteem on meile tuntud kümnendsüsteem, kus protsent tähendab suhet saja osa suhtes
-duodetsimaalsüsteem e. kahetestkümnendsüsteem e. tollsüsteem lähtub pikkusühiku - 1 jala - jagunemisest 12 tolliks, mis jaguneb omakorda pool-, veerand- ja  1/8-tollideks - viimaseid on ühes jalas 96. (1/8" oli enamasti vähim jaotis, 1/16" ja 1/32" jagati edasi silma järgi).
  
                                                                                                                                                                        tagasi sisukorda





Kaaremõõdikud  mõõtsid nurka mõõteriista kaareskaala abil:  nurk fikseeriti  kahe viseerimishaara abil, lugem võeti kaareskaalalt. vt. album


1677
1597		 Kvadrant oli kaaremõõdik, mille kaare pikkuseks oli veerand täisringi (90°)                                                                                                                                                                                                                                                                                                                                                            

                                                          


16. sajandi lõpp
17. sajandi algus             		  Grafomeeter oli kaaremõõdik, mille kaare pikkuseks   oli pool täisringi  (180°)               
MÄRKUS: grafomeetri ühel viseerimishaaral  esineb sageli kompass. Kui selle haara asendit ei fikseerita kaareskaala, vaid kompassi nõela järgi, siis kasutatakse grafomeetrit bussoolina. Sellisel moel kasutati  grafomeetrit allmaatöödel.

 Bussool  aastast 1667
(puidust korpusega)           		 Bussool 1600  Bussool on tänapäevane nimetus    kaaremõõdikule,   millel on vaid üks sihik,  lugem võetakse kompassi skaalalt (väline kaareskaala puudub).  Suure kaareskaala täpsusele jääb kompassiskaala kindlasti alla, kuid bossooli oli mugav kasutada maa-alustes käikudes.                                                                                                                                                                                                     

 
Teodoliit aastast 1586  		Astrolaab 1551
  Teodoliit ja astrolaab olid kaare pikkusega 360°                                   
Teodoliit aastast1586 võis  anda ühtaegu nii horisontaalse kui ka vertikaalse nurga lugemid. 

                                                                                                                                                                           tagasi sisukorda






4.  Geodeesia instrumendid  maa-aluses sõjas.

Allmaatöödel kasutatud mõõtelauad ja nurgamõõdikud olid varustatud kompassiga, kõige spetsiifilisem allmaatööde mõõteriist oli seetõttu bussool.
Instrumentidega töötamise selgituseks olgu  kirjeldus käigu plaanistamisest mõõtelaua abil (suurem ja kohmakam instrument, kuid plaan sai valmis kohe viseerimise käigus).
    



http://hdl.loc.gov/loc.rbc/
rosenwald.1363		 Selleks, et juhtida käigu kaevajad sihile, tuleb kaevajate liikumine plaanistada.
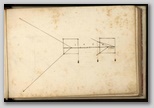
1) Mõõtelaual valmistatakse kolmnurki konstrueerides plaan, millel on sihtmärk (bastioni nurkgad), seejärel kantakse  plaanile ka  maa-aluse käigu sissepääs
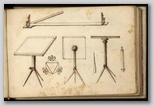
2) Mõõtelaua asendit  muutmata kinnitatakse lauale kompass ning märgitakse plaanile nõela suund
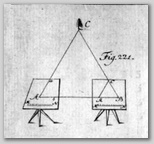
3) Käiku sisenedes pannakse laud  madalale alusele ja pööratakse kompassi järgi õigeks 
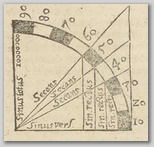
4) Viseerimisjoonlaua abil näidatakse kaevajatele suund,  läbitud vahemaa  mõõdetakse ning  kantakse mastaapskaala ja  mõõtesirkli abil plaanile
5) Kui käigul tekib suunamuutusi, seatakse laud iga käänaku kohal uuesti üles ja orienteeritakse kompassi järgi. Kui laua asukoht on märgitud plaanile, jätkatakse edasi nagu pp. 3-4.

Mõõtelauaga sisenemisel kitsasse käiku tuli kolmjalg eemaldada, madala alusena soovitatakse näiteks trummi.

Maa-alustel kaevamistel oli väga oluline jälgida kõigu kaldenurka, seetõttu tuli plaanistada ka käigu vertikaallõige, kaldega käikudesse pingutati mõõteköisi, köie kaldenurga mõõtmiseks kasutati rippuvaid nurgamõõdikuid.
    Kaldenurga mõõdik on näha ka Pretorius&Schwenters´i mõõtelaual. 

                                                                                                                                                                        tagasi sisukorda