Tartu Ülikool

Filosoofiateaduskond

Ajaloo-osakond

Arheoloogia õppetool

 

 

 

 

 

 

Tanel Saimre

Raskusjõul töötava heitemasina analüüs ja rekonstruktsioon

 

Bakalaureusetöö

 

Juhendaja Ain Mäesalu

 

 

 

 

 

 

 

 

Tartu 2005

 

Sisukord

 

1.     Sissejuhatus.............................................................................................................. 3

1.1        Töö tutvustus.......................................................................................... 3

1.2        Heitemasinate rollist ajaloos..................................................................... 4

1.3        Allikad ja uurimused................................................................................ 5

1.4        Terminoloogiast....................................................................................... 7

2.     Heitemasinad üldiselt – nende tüübid......................................................................... 9

2.1        Vetruva puuvarva elastsusjõul töötavad heite- ja laskemasinad............... 10

2.2        Köiekimpude väändejõul töötavad masinad ehk torsioonmasinad........... 12

2.3        Raskusjõul töötavad heitemasinad ehk blided......................................... 15

3.     Vastukaaluga blide mehaanika................................................................................. 19

3.1        Masina ehitamisel määratavad tegurid.................................................... 23

3.2        Masina kasutamise käigus määratavad tegurid........................................ 26

3.3        Laskekiirus, täpsus ja töökindlus............................................................ 28

3.4        Laskemoonast....................................................................................... 29

3.5        Võrdlus teiste masinatüüpidega.............................................................. 31

4.     Blide rekonstruktsioonid......................................................................................... 32

5.     Kokkuvõte............................................................................................................. 39

6.     Kasutatud allikad ja kirjandus................................................................................. 41

7.     Lisa 1: joonised...................................................................................................... 43

8.     Summary: Analysis and Reconstruction of a Counterweight Trebuchet...................... 54

 

1.              Sissejuhatus

Ja Uskija valmistas neile, kõigele sõjaväele, kilpe ja piike ja kiivreid

 ja raudriideid ja ambusid ja lingukive. Ja tegi Jerusalemma osava mehe

 osavasti mõeldud sõjamasinaid, mis pidid olema tornide peal ja müüri

 nurkade peal, nooltega ja suurte kividega lasta. Ja ta nimi sai kuulsaks

 kaugele, sest ta sai abi imelikul kombel, seni kui ta sai vägevaks.

Teine Ajaraamat 26:14-15, Vana Testament

1.1                      Töö tutvustus

Käesolevas uurimuses on võetud vaatluse alla Euroopas keskajal kasutatud heitemasinad. Tuuakse esile erinevat tüüpi masinate kohta olemasolev materjal ja iseärasused. Analüüsitakse laiemalt kõiki tuntud masinaliike ning seejärel keskendutakse vastukaalu jõul töötavale heitemasinale ehk blidele, kui ajaliselt kõige viimasele ning tehniliselt kõige arenenumale heitemasinaliigile. Võetakse vaatluse alla katsed blide rekonstrueerimise alal ning uuritakse antud masinatüüpi mehaanika vaatevinklist. Töö eesmärgiks on lähendada heitemasinate ajaloo-alastes uurimustes olevaid teadmisi tänapäeva füüsikateaduse poolt pakutavatele võimalustele, lootuses leida midagi ajaloo-uurijatele kasulikku.

Uurimuses kasutatav materjal on pärit teaduslikust kirjandusest, blide rekonstruktsiooniga läbiviidud katsetest ning arvutiprogrammi WinTrebStar 4.0 abil sooritatud simulatsioonkatsetest. Mõnevõrra kasutatakse ka internetist pärit informatsiooni.

Teemavaliku tingis eeskätt autori kogemus nii sõjatehnika ajaloo kui ka füüsikateaduse alal ning fakt, et antud teema on Eestis seni suhteliselt vähe käsitlust leidnud. Lisaks avanes autoril 2002. aasta suvel meeldiv võimalus Otepää Lions klubi toetusel ehitada raskusjõul töötava heitemasina ehk blide täissuuruses rekonstruktsioon ja sooritada sellega heiteid. Nimetatud masin oli autori jaoks praktiline õppevahend blide „hingeelu” tundmaõppimiseks ja teatud vilumusegi saavutamiseks vastukaalu-heitemasinaga opereerimisel. Sellest lähemalt juba blide rekonstruktsioone käsitlevas peatükis.

Uurimuse kronoloogilised piirid ei ole täpselt määratud. Vaadeldakse peamiselt keskaegseid masinaid kuni nende väljatõrjumiseni tulirelvade poolt, kuid tehakse ka võrdlevaid põikeid ühelt poolt roomaaegsete ning teiselt poolt hilisemate heiteseadeldiste juurde. Territooriumiks on väheste eranditega Euroopa.

Sissejuhatuses analüüsime üldisemaid küsimusi nagu seniseid selleteemalisi uurimusi, terminoloogiat jms. Esimeses peatükis võtame ükshaaval vaatluse alla kõik tuntud masinatüübid, liigitatuna tööprintsiibi alusel. Analüüsime ka erinevate autorite jooniseid. Selle osa eesmärgiks on tutvustada lugejale heitemasinate mitmekesisust ning funktsionaalseid erinevusi – tavainimese teadmistes on kahjuks juurdunud varasematest ajalooõpikutest pärit üks „tüüpheitemasina” pilt, mida peetakse üldlevinuks kogu püssirohueelsel ajastul. Teises peatükis siirdume vastukaalu jõul töötava heitemasina täpsema käsitluse juurde ja seletame lahti selle füüsikalised printsiibid. Käime välja mõned tõed ja rakendused, mida ka ajaloo-uurijad lihtsasti kasutada saaksid. Kolmandas peatükis vaatleme blidede rekonstrueerimisel tehtud katseid ja uurime sel alal saavutatut. Muuhulgas kirjeldame ka autori enda poolt läbi viidud rekonstruktsiooni Otepää linnamäel. Seome rekonstruktsioonkatseid eelnevas peatükis esitatud füüsikalise käsitlusega.

1.2                      Heitemasinate rollist ajaloos

 

Kogu oma eksisteerimisaja vältel on inimesed omavahelistele lahkhelidele vägivalla abil lahendust otsinud. Pidevalt on mõeldud välja uusi ja huvitavaid viise, kuidas vaenlastele kahju teha. Parimaks illustratsiooniks sellele on sõjatehnika. Sõna engin, millega tähistati keskajal sõjamasinaid, tulenes sõnast ingenium – geniaalne seadeldis, nupukas sepitsus. Nähtavasti olid keskaegsed inimesed ise (vastupidiselt tänapäeva üldsusele) oma sõjariistadega rahul ja tundsid nende üle uhkustki. Mehed, kes oskasid heitemasinaid ehitada ja käsitseda, olid hinnatud ja austatud. Tänapäeva inglise keeles kohtame sõnu engine, mis tähendab mootorit; ning engineer, mis tähendab inseneri. Kas nende sõnade kasutuselevõtus on oma rolli mänginud ka sõjamasinad ja nende meistrid?

On enam kui kindel, et heitemasinad aitasid  otseselt kaasa inimese teadusliku maailmapildi ja tehnoloogia arengule. Masinate ehitamise ja kasutamise tõttu sagedastes sõdades puutusid inimesed otseselt kokku tol ajal lahendamata küsimustega mehaanika ja elastsusjõudude alal. Näiteks omandas blide vastukaal masina arengu viimastes faasides spetsiifilise kuju (vt. joonis 1). Matemaatikas tuntakse sellist kujundit salinon’i ehk soolatoosi nime all (vt. joonis 2). Taolise kuju korral kontsentreerus suurem osa vastukaalu massist riputuspunktist võimalikult kaugele, samas ei olnud vaja vastukaalu ja masina raami vahele niivõrd palju vaba ruumi jätta. Peatükis 3.1 näeme, et mida kaugemal ripub vastukaal oma kinnituspunktist, seda paremini masin töötab. Sarnase kujuga vastukaale kohtame ka paljudes hilisemates masinates, mis kasutavad pendlit – näiteks pendlijõul töötavad saed. Kuigi pendli füüsikaliste omaduste avastamist seostatakse eelkõige Galileo Galileiga, võib tõendeid pendli kasutamisest kellades leida juba Leonardo da Vinci’le lähedase kellasseppade perekonna poolt. Da Vinci märkis ka ise korduvalt, et mitmed tema leiutised võimaldavad täpselt aega mõõta (Chevedden jt. 1995: 62-63).

12.-13. sajandi üks tähelepanuväärsemaid arenguid teoreetilise mehaanika alal leidis aset tänu Jordan Nemorariuse (suri umbes 1237. a.) tööle. Tema töötas välja kangi teooria, mille aluseks on saadud ja kulutatud töö võrdsuse printsiip (Piir 1996: lk 10). Jordan väitis ka, et mass, mis langeb vertikaalset trajektoori mööda, on võimeline tegema rohkem tööd, kui mass mis langeb võrdse vahemaa maa suhtes diagonaalselt. Seos vastukaalu jõul töötava heitemasinaga on siin ilmne. Masinameistrid teadsid, et rippuva vastukaaluga masin heidab kivi kaugemale, kui võrdse jäigalt heitekangi külge kinnitatud vastukaaluga masin (Chevedden jt. 1995: lk 63).

1.3                      Allikad ja uurimused

 

Huvi keskaegse sõjatehnika ja relvastuse vastu on viimaste aastakümnete jooksul märgatavalt kasvanud. On tekkinud arvukalt nii „tagaõue-insenere” kui ka professionaalsemaid huvilisi, kes tegelevad kõigega, mis seondub keskaja ja sõjapidamisega, sealhulgas ka heitemasinate ehitamise ja uurimisega. USA-s korraldatakse lausa iga-aastaseid heitemasinate võistluseid kõrvitsate heitmises. USA Patendiameti kodulehelt (www.uspto.gov) võib otsingu „trebuchet” järgi leida vastukaalu jõul töötava lõbustuspargi-atraktsiooni inimese heitmiseks. Seoses sellise populaarsusega on internetis saadaval suurtes kogustes antud teemat käsitlevat materjali, on üles seatud isegi blide-huvilistele mõeldud portaal (www.trebuchet.com). Kahjuks on enamik sellest materjalist, nagu interneti materjalide puhul ikka, teaduslikus mõttes kasutu – ei ole viidatud allikatele, tihti kohtab ilmselgeid liialdusi, ajaloolist tõepära pole eesmärgiks seatud ega sellest ka kinni peetud. Kui välja arvata napp teaduspublitsistika alla liigitatav osa, kujutab enamik internetis olemasolevat materjali endast parimal juhul huvitavat lugemist, kuid mitte enamat.

Üks olulisemaid teoseid antud töö koostamisel on sir Ralph Payne-Gallwey 1903. aastal ilmunud monograafia „The Crossbow”, millele on lisatud rikkalikult illustreeritud ja kommenteeritud heitemasinaid käsitlev osa. Kuigi raamatut võib pidada mitmes mõttes vananenuks, kujutab ta endast siiski ka tänapäeval suurt väärtust. Teiseks oluliseks uurimust kujundavaks materjaliks sai Ain Mäesalu ilmumisel oleva monograafia käsikiri "Ammud, laske- ja heitemasinad muistses vabadusvõitluses ja keskaegses Eestis". Nende kahe ning terve rea vähemmahukate uurimuste abil koostati ülevaade teema ajaloolisest aspektist.

Mehaanikalise käsitluse kohta leidub materjali märksa napimalt. Suureks abiks autorile oli kaks internetis avaldatud artiklit: Donald Siano „Trebuchet Mechanics” ja W. E. Jahsmani „The Counterweighted Trebuchet – an Excellent Example of Applied Retromechanics”. Need mõlemad on kahjuks trükitud kujul ilmumata, ent sellegipoolest väga põhjalikud analüüsid.

Donald Siano koostatud raskusjõul töötava heitemasina simulaatoriga WinTrebStar 4.0 viis autor läbi suure hulga katsetusi, mille tulemused olid samuti olulisel kohal paljudele järeldustele jõudmisel.

Teema uurimist raskendavaks asjaoluks on kindlasti igasuguse arheoloogilise leiumaterjali puudumine. Erinevalt käsirelvadest ja turvistest olid heitemasinad liiga suured, et ühes tükis meie ajani säilida. Saksa uurija B. Rathgeni teatel olevat 1890. aastal Ida-Preisimaal Liebenmühlis vana kiriku lammutamisel küll üks terve masin leitud, aga kahjuks kasutati see kohalike elanike poolt koheselt küttepuudena ära (Hansen 1992: 193). Seetõttu peame tuginema kaudsetele andmetele – näiteks 2000. aastal Viljandi linnuse kaevamistel leitud kiviheitemasina alusrajatise (Valk 2001) sarnastele leidudele ning loomulikult kirjalikele allikatele ja eksperimentaalarheoloogia tulemustele.

1.4                      Terminoloogiast

Täpse ja ainuõige terminoloogia paikapanek on antud teema uurimisel üks keerulisemaid  probleeme. Illustratsiooniks sellele väitele lisan siia kaunis meelevaldse loetelu kogutud nimetustest, mida on erinevates allikates kasutatud laske- ja heitemasinate kohta:

(Payne-Gallwey 1903: 250; Hansen 1992: 191)

 

Paljusid neist võib kindlasti pidada ühe ja sama termini erinevateks vormideks (näiteks blida ja blide, springala ja espringala,  trabuchium ja trebuchet). Siiski on erinevate autorite poolt ja erinevatel aegadel kasutud termineid suhteliselt palju.  Võis ju iga autor kasutada ühe ja sama masinatüübi kohta erinevat nimetust. Võimalik on ka vastupidine variant – üks nimetus võib erinevates allikates tähendada erinevaid masinatüüpe. Sarnaselt eestikeelsele sõnale „suurtükk”, mis tähistab kõikvõimalikke selle relva tüüpe ja arendusi alates suurtüki leiutamisest kuni tänapäevani välja, on ka keskaegsete heitemasinate nimetused tihti olnud ajas muutumatud, kuigi nimetusega tähistatav relvaliik on edasi arenenud. Pealegi on allikates kasutatud sageli üldistavaid nimetusi. Näiteks Henriku Liivimaa kroonikas räägitakse lihtsalt „masinatest” (lad. k. machina). Bütsantsi allikates kasutatakse nimetust helepolis, mis tõlkes tähendab lihtsalt „linnavallutajat” või „-võtjat” ja mida on arvatavasti kasutatud vaheldumisi nii heitemasinate kui ka piiramistornide ja isegi muu piiramistehnika kohta. (Dennis 1998: 100). Tegelikult on pilt veelgi segasem, sest omal ajal tarvitati tähelepanuväärsemate masinate kohta ka personifitseerivaid nimesid: Metskass, Leedi, Kuninganna, Sõjahunt jmt (Payne-Gallwey 1902: 250). Järgnevas paneme siiski kirja üldlevinumad nimetused, et püüda luua erinevate terminite seas mingisugust koherentsust.

 

Raskeambude kõige levinuma nimetusena oli kasutusel ballista ja selle versioonid, kusjuures see termin on ühtlasi ka tänapäeval kõige juurdunum. Manuballista tähendas käes hoitavat raskeambu (mis järelikult ei saanud väga raske olla) või siis ka lihtsalt ambu. Väikesel hobuvankril asetsevat raskeambu on nimetatud carroballistaks (Dennis 1998: 99).

Torsioonjõul töötavaid masinaid märgiti märksa enamate nimedega. Levinuim termin – katapult – tähistas üheõlalist torsioonmasinat. Muide termin ise tuleneb sõnadest peltē, mis tähistas Kreeka sõjamehe kilpi ja kata, mis tähendab allapoole suunatud lööki või liikumist. (Soedel, Foley 1979: 123). Rooma sõdurid olevat alguses sama masinat tähistanud nimega onager, mis tähendab tõlkes metseeslit (nähtavasti jõnksatuse või hüppamise tõttu, mida masin lasu ajal tegi). Hiljem võtsid ka nemad kasutusele nime katapult (Mäesalu 2005). Kahjuks on katapuldist tänapäeval saanud igasuguste vanaaegsete heite- ja laskemasinate üldnimetaja.

Kahekangiliste torsioonmasinate osas pakub Ain Mäesalu välja huvitava teooria. Nimelt termin notstal tähendas algselt puurilaadset seadeldist, mida kasutati tõrksa hobuse paigal hoidmiseks rautamise ajal („notstal” tähendaks otsetõlkes „hädatall”). Mõnel keskaegsel joonisel on kujutatud samuti puurilaadse tugistruktuuriga kahekangilisi torsioonjõul töötavaid nooleheitemasinaid, mida nähtavasti välise sarnasuse tõttu hakati samuti notstaliks nimetama. Angarium on sama sõna ladinakeelne vaste (Mäesalu 2000: 15-16). Tihti tähistatakse neid masinaid ka sõnaga ballista, kuid selguse mõttes eelistab autor kasutada siinkohal siiski muid termineid – lisaks ülalmainitud kahele (mis tähistavad spetsiifilise kujuga masinaid) kasutame terminit springala.

Raskusjõul töötavate masinate tähistamiseks on eriti inglise keelt kõnelevates maades viimasel ajal hakanud levima termin trebuchet. Algselt tähistati sellega tegelikult vaid kõige suuremaid taolisi masinaid. Trabucium, trabuchus, tripantium, trebusket jt kujutavad selle sama sõna eri vorme. Tõenäoliselt tähendas see kolme jalga, mis on arvatavasti jällegi vihje masina välisele kujule. Tavaliselt toestasid suuremaid vastukaaluga masinaid külgedelt kaks tuge, ja heitekang ise, mis vinnastatud olekus oli otsaga vastu maad, kujutas kolmandat jalga (Chevedden 2000: 100).

Kuna Eestis nagu ka Saksamaal ja Skandinaavias on nende masinate kohta läbi keskaja kasutatud terminit blide, siis jääme siinkohal (ühtlasi ka  lihtsuse ja suupärasuse tõttu) sama nimetuse juurde.

2.              Heitemasinad üldiselt – nende tüübid

Ajaloo jooksul kasutatud küllalt erinevad heitemasinad sunnivad looma nende tüpoloogiat, mille abil saaks üldisesse pilti natuke korda luua. Senistes uurimustes on heitemasinaid liigitatud mitmeti. Vanemas kirjanduses käsitletakse masinaid nende omaaegsete nimetuste järgi. Inglise sõjaajaloolane ja eksperimentaator sir Ralph Payne-Gallwey jaotab vanaaegsed heite- ja laskemasinad oma monograafias „The Crossbow” kolme suurde klassi: balista, katapult ja trebuchet. Selline lähenemine on küll mõistetav, sest oli ju tol ajal põhiline huvi seletada lahti vanadest allikatest pärit erinevate nimetuste taga peituvad masinad. Ometi tekitab see palju probleeme. Nimelt, nagu sissejuhatuses mainitud, pole paljude nimetuste tähendus sugugi üheselt lahti mõtestatav.

Saksa uurija Volker Schmidtchen pakub välja liigituse vastavalt masinate suurusele (Schmidtchen 1983). Väiksemaid masinaid nimetab ta ballistideks ja suuremad katapultideks. Ka see liigitus pole kõige parem, sest ühte tüüpi masinaid ehitati vahel erinevates suurustes. Schmidtcheni liigituse kohaselt kuuluksid seega mõned konstruktsioonilt sarnased masinad kahte erinevasse klassi.

Relvastusuurija Ain Mäesalu pakub välja masinate liigituse tööprintsiibi alusel. Ta eristab kolme rühma: vetruva puuvarva elastsusjõudu kasutavad mehhanismid, nöörikimpude väändejõul põhinevad laske- ja heitemasinad ning raskusjõudu kasutavad heitemehhanismid (Mäesalu 2005).

Selline liigitus, kui masinate mehhaanikalist olemust kõige lähemalt järgiv, sobib hästi kokku käesoleva uurimistöö rõhuasetusega ja võetakse ka järgneva analüüsi aluseks.

Esimese kahe rühma masinad töötavad elastsusjõu[1] mõjul. Masina vinnastamisel painutati vetruvat puuvarba või muud elastset keha (esimese rühma masinate puhul) või väänati köiekimpude vahele kinnitatud heitekangi või kange (teise rühma masinate puhul). Selle tulemusena salvestus vinnastamisel tehtud töö potentsiaalse energia näol masinasse. Päästiku vabastamisel muundus see energia üle heidetava keha kineetiliseks energiaks. Kolmanda rühma masinad töötasid vastukaalu jõul – vinnastamisel tõsteti vastukaal üles, salvestades niimoodi jällegi masinasse energiat. Masina vallapäästmisel vajus vastukaal alla ja andis oma energia üle heidetavale kehale.

On üldlevinud seisukoht, et esimese kahe rühma esindajaid tunti juba antiikajal. Vetruva puuvarva elastsusjõul ehk ammu põhimõttel töötavate masinate ilmekaimaks näiteks on raskeamb, mis kujutas endast lihtsalt hiiglaslikku ambu, paigutatuna vastavale alusele, mis hoidis masina maapinnast sobival kõrgusel ja võimaldas ka sihtida. Köiekimpude väändejõudu ehk torsioonjõudu rakendavad masinad on tänapäeval tõenäoliselt kõige laialdasemalt tuntud.

Kolmas rühm ehk raskusjõul töötavad masinad on aga just keskaegse sõjatehnika suurim saavutus. Oma lihtsa ja seetõttu vastupidava konstruktsiooni tõttu levisid nad laialdaselt ja tõrjusid teised heitemasinad pikapeale välja. Kui palju esimese kahe rühma masinaid keskajal kasutati ja millisel määral nad raskusjõul töötavate masinatega asendusid, on siiani vaidlusalune küsimus. Selge on see, et raskusjõul töötavad masinad olid keskaja võimsaimad relvad ja isegi peale püssirohu kasutuselevõttu võistlesid need edukalt algeliste suurtükkidega.

2.1                      Vetruva puuvarva elastsusjõul töötavad heite- ja laskemasinad

 

Antud rühma kõige iseloomulikumad esindajad olid raskeammud, mis kujutasid endast suuri ambe paigutatuna vastavale alusele. Raskeammule sarnaste masinate kasutamisest on märke juba antiikajal (Soedel, Foley 1979: 120), selle masinatüübi kõige varasemaks näiteks võib pidada 4. saj. e. Kr.  Kreekas leiutatud relva nimetusega gastraphetes. Schmidtchen peab seda ka tavalise ammu eelkäijaks (Schmidtchen 1983: 105-106).

Hiiglasliku ammukaare elastsusjõul töötavad masinad saavutasid pikkamööda oma arengu tipu, aga mõningase kohmakuse ja väikese võimsuse tõttu võitsid nende kõrval peagi suurt populaarsust torsioonmasinad. Peale Rooma riigi langemist pole raskeambude kasutamisest ühtegi märki kuni 13. sajandini. Keskajal kasutati raskeambe põhiliselt kaitserelvana linnades ja kindlustustes, millest tulenesid ka nimetused nagu müüriamb, jalaga amb jne (Schmidtchen 1983:  109). Sageli on aga nende hulgas raske piiri tõmmata suure käsiammu ja väikese laskemasina vahele.

Põhimõttelise ettekujutuse raskeammust annab joonis 3. Da Vinci poolt kujutatu näeb välja küll väga muljetavaldava relvana , kuid on põhjust arvata et reaalselt sellist masinat siiski kunagi eksisteerinud ei ole.

Joonist analüüsides tuleb kõigepealt tunnistada, et tegemist on läbimõeldud kavandiga. Alustame ”jõuallikast” endast – nagu näha on ammukaar konstrueeritud mitmest erinevast kihist, mis aitab vähendada kaare sisemisi pingeid paindesoleku ajal ja vältida kaare murdumist. Samuti saab valida kõige paremini sobivad materjalid – kaare väliskihi valmistamisel võib kasutada elastseid puuliike, sisemiste puhul jällegi kõvemaid ja tugevamaid. Päästikusüsteemidest on joonise vasakus osas esitatud suurendatuna kaks varianti. Mõlemas kasutatakse käsiambudele analoogilist päästikuketast. Vinnastatud raskeammu kõrval seisev inimene ongi parajasti vajutamas päästekangile.

Erilist tähelepanu väärib vinnastamissüsteem. Kodarad, millest vinna keeratakse, on äärmiselt lühikesed ja nii võimsat ambu ei oleks inimene kindlasti võimeline vinnastama. Nähtavasti on da Vinci siiski sellele ka mõelnud. Paremal suurendatuna kujutatud hammasratta ja vintlati süsteemi pakutakse ilmselt ülekandesüsteemina (analoogselt tänapäeva käigukastidele), mis võimaldab vähendada jõudu millega vintsi keeratakse ja suurendades selle arvelt vajalike vintsipöörete arvu. Taolist ülekandesüsteemi rakendades võtaks raskeammu vinnastamine jällegi äärmiselt kaua aega.

Da Vinci kujutatud raskeamb arvatavasti töötaks, iseasi, kas ta ennast lahingutegevuses ka õigustaks. Kas selle hiiglasliku ja keerulise masina lahinguomadused on väärt neid ressursse ja vaeva mis tema valmistamiseks ning transpordiks kulub? Arvatavasti mitte. Payne-Gallwey on seisukohal et hiiglasliku ammukaare elastsusjõudu kasutavad masinad on kohmakad ning raskesti sihitavad, transporditavad ja hooldatavad. Tema arvates ei kasutatud selliseid masinaid kunagi. Eksisteeris küll ammulaadseid sõjamasinaid suurte noolte lennutamiseks, kuid neil oli ammukaar asendatud kahe iseseisva poolkaarega, mis töötasid köiekimpude väändejõul (Payne-Gallwey 1903: 302), aga neid analüüsin lähemalt juba järgmises osas.

Teine joonis,  mida on samuti väga usinasti publitseeritud, kujutab mõnevõrra usutavamas suuruses raskeambu (joonis 4). Sellel esitatakse ka huvitav idee, mille kohaselt ammukaar ei koosne kahest poolest nagu tavaliselt, vaid lausa kuuest painduvast latist: kahest horisontaalsest ja neljast vertikaalsest.

Paraku esineb ka viidatud joonisel vigu: üks mees ei suudaks niivõrd väikese vintsi abil sellist masinat kindlasti vinnastada. Masina kõrval maas näeme nii nooli kui ka kuule või kive. Nähtavasti tahab autor öelda, et laskemoonaks kõlbasid mõlemad.

Allikad kinnitavad, et raskeambudega lasti kindlasti suuri, oda meenutavaid nooli ja ka süütenooli. Kuna nool on võrdse kaalu puhul kivist märksa ohtlikum, siis kivide kasutamine laskemoonana on antud masinatüübi väikese võimsuse tõttu väheusutav.

 

Vetruva puuvarva elastsusjõul töötavate heitemasinate iseloomustuseks võib öelda, et tegemist oli antiikajal levinud liigiga, mille kohta keskajal on suhteliselt vähe täpsemaid teateid. Pealegi jäävad need oma laskeomadustelt alla köiekimpude väändejõul töötavatele masinatele, aga veelgi enam vastukaalu-masinatele. Väiksemad eksemplarid olid 13.-16. sajandil siiski kasutusel , kuid neid saab heitemasinateks (õigemini laskemasinateks) nimetada vaid tinglikult. Kujutasid nad endast ju lihtsalt suuremat sorti ambe, mis laskmisel toetati müürile või spetsiaalsele alusele.

2.2                      Köiekimpude väändejõul töötavad masinad ehk torsioonmasinad

Selle rühma esindajate näol on tegemist märksa arenenuma masinaliigiga kui raskeammud. Hiiglasliku ammukaare asendamine köiekimpudega andis võimaluse ehitada palju kergemaid ja võimsamaid masinaid. Keerdpingestatud köiekimp on ju palju lihtsam, kompaktsem ja kergem kui suur puidust või metallist kaar. Kuna keerdpingestatud köiekimp kujutab endast füüsikaliselt võttes torsioonvedru, siis nimetame edaspidi köiekimpude väändejõul töötavaid masinaid lihtsama ja lühema sõnaga torsioonmasinad.

Antud liigi alla kuuluvad masinad saab jagada ühe- ja kahekangilisteks. Ühekangilistel masinatel oli horisontaalselt asetatud köiekimbu vahele pistetud heitekangi üks ots ja tema teises otsas asus kulp heidetava kivi jaoks. Kahekangilistes masinates kasutati kahte vertikaalset paigutatud köiekimpu, millesse pistetud kangid olid omavahel ühendatud nööriga ja moodustasid ammule sarnase mehhanismi.

 

Ühekangilised torsioonmasinad eksisteerisid kindlasti juba antiikajal. Rooma arhitekt ja sõjaväeinsener Vitruvius Pollio on kirja pannud juhised 162-kilogrammiseid kive pilduva masina ehitamiseks. Arvata on, et seda masinat reaalsuses kunagi valmis ei ehitatud, küll aga väiksemaid (Soedel, Foley 1979: 120).

Ühekangilise torsioonmasina põhiliseks detailiks oli heitekang, mille ülemises otsas asus kausi- või kulbilohku meenutav süvend, millesse asetati kivikamakas. Kangi alumine ots asetses eelnevalt keerdpingestatud köiekimbu vahel. Kui kangi ülemine ots tõmmati vintside abil alla, siis salvestati köiekimpu lisapinge näol potentsiaalset energiat. Päästiku vabastamisel pöördus heitekang suure kiirendusega ümber oma alumise otsa ja paiskas kivi teele. Joonis 5 on suhteliselt realistlik, kuigi masin tundub tõhusaks piiramistegevuseks olevat väiksevõitu (Payne-Gallwey 1903: 267). Teiseks oluliseks puuduseks on päästemehhanismi puudumine. Samuti ei ole näidatud, kuidas vabastatakse enne lasku masina vinnastamiseks kasutatav köis, mis jookseb ümber heitekangi küljes oleva ploki. Plokk kergendab vinnastajate tööd poole võrra – kaks korda rohkem köit on vaja ümber vintsi keerata, mis tähendab et iga pööre vintsiga on kaks korda kergem.

Joonis 5 võib hästi näha, et heitekang on mässitud köie sisse. Kuna heitekang sai iga löögiga väga tugevalt põrutada, siis ei saanud teda valmistada lihtsalt monoliitsest palgist. Payne-Gallwey annab edasi kogemused, mis ta oma mudelite ehitamise ja katsetamise käigus sai. Kõige sobivam puit olevat nii heitekangi kui põikpuu (mille vastu heitekang lajatab) valmistamiseks saar. Heitekangi alumises otsas peaks olema jämedam osa (joonis 6, E), muidu kipub heitekang köite vahelt välja libisema. Heitekangi soovitab Payne-Gallwey valmistada kolmest osast. Kõigepealt tuleb valida kolm siledat ja omavahel hästi sobivat prussi, ilma vigade ja oksakohtadeta. Need on vaja kokku liimida ja tappida ning vormida nii, et nad moodustaksid enam-vähem ümmarguse ristlõikega tala. Seejärel mähiti kogu tala ümber liimiga määritud tugeva linase riide ribad ja soovitavalt mitme kihina. Sinna peale keriti omakorda liimi sisse kastetud tugev nöör. Protseduur meenutab liitvibu valmistamist ja lõpptulemusena saadav heitekang on palju elastsem ja tugevam kui monoliitne palk (Payne-Gallwey 1903:  279-287).

Põhiliseks küsimuseks ühekangilise torsioonmasina ehitamisel oli vajaliku köiekimbu läbimõõt, mis kindlustaks masina võime efektiivselt opereerida. Aastal     270 e. Kr. töötas grupp kreeka insenere välja valemi, mille abil vajalikku läbimõõtu arvutada:

 

 

d – köiekimbu vajalik läbimõõt daktülides (1 daktül ≈ 2 cm)

m – heidetava kivi mass miinades (1 miin ≈ 440 g)

 

Seega kui sooviksime ehitada käesoleva osa alguses mainitud 162 kg kive pilduva masina, peaks selle köiekimbu läbimõõt olema 73 cm.

 

Kahekangiline torsioonmasin meenutab mõnevõrra raskeambu. Osadel masinatel võis laskejõud mingil määral tuleneda ka kangide elastsusest, kuid põhiline osa energiast talletati siiski köiekimpudesse, mille vahel kangide otsad asetsesid.

Joonis 7 kujutab kahekangilise torsioonmasina näidet. Pildil on kahjuks hulgaliselt puudusi. Sellise masinaga ei saaks kive kindlasti loopida kuigi kaugele. Olukorda võiks parandada see, kui masin oleks sihitud kõrgemale ja kivid lendaks kaarjamat trajektoori mööda. Samas jääb pilti vaadates  arusaamatuks, kuidas (või kas üldse) sai seda masinat üles-alla sihtida?. Kivi on asetatud lihtsalt vastu köisi, mis tähendab, et köied saavad iga lasuga hõõruda. Poleks olnud ju raske valmistada näiteks nahast polstrit, mis köie ja kivi vahele asetada. Kolmandaks puudub joonisel mehhanism masina vinnastamiseks. Pildilt näib, et masinat vinnastati eraldi vintsiga, mis asetses masinast eemal, kuid sel juhul peaks masin olema tugevasti maa külge kinnitatud, et ta vintsi tõmbele järele ei annaks.

Joonis 8 kujutab Rooma kahekangilist torsioonmasinat Payne-Gallwey pilgu läbi. Tegemist on märksa läbimõelduma seadeldise kujutisega. Laskemasin on parajasti vinnastatud ja noolega laetud. Masina konstruktsioon võimaldab üles-alla sihtimist ja tema proportsioonid on õiged. Päästikumehhanismi pole küll hästi näha, ent selleks näib olevat taas midagi käsiammu päästikuketta laadset.

Selle masina juures võib näha üht huvitavat uuendust – köiekimpude otstes asuvate hammasrataste abil saab reguleerida neis valitsevat pinget – s.t. vinnastamisel vajaminevat jõudu ja noole lennukaugust.

Joonisel esitatakse detaile rohkem, kui neid on ajalooliste allikate võimalik kindlaks teha. Nii  pole säilinud ühtegi tõendit, mis näitaks, et säärane köiekimpude pinge seadmise mehhanism ka reaalselt eksisteeris. Samas pole sellises täiustuses midagi ületamatult keerulist ja on usutav, et omal ajal selle peale tuldi.

Suuremat sorti kahekangiline heitemasin kujutas endast võimast relva. Payne-Gallway on oma konstrueeritud mudelite, ajalooliste allikate ja arvutuste põhjal hinnanud, et joonisel kujutatud masin võis lennutada nooli 400 - 450 jardi (366 - 412 m) kaugusele. Kujutatud masina köiekimpude läbimõõduks on  8 tolli (20 cm). Suurimal Payne-Gallwey poolt konstrueeritud kahekangilise masina mudelil olid kangid 61 cm pikad ja köiekimbud 7.6 cm läbimõõduga. Masin oli võimeline 1.1 kg kaaluva oda lennutama 274 m kaugusele. Oma kerguse, kompaktsuse ja kerge sihitavuse tõttu kasutati kahekangilisi heitemasinaid kindlustatud punktide kaitsmise kõrval ka välilahingutes. Võib lugeda juhtumitest, kus heitemasinast lastud nool tungis läbi mitmest mehest korraga, teinekord naelutati turvises mees puu külge kinni (Payne-Gallwey 1903: 303).

2.3                      Raskusjõul töötavad heitemasinad ehk blided

 

Raskusjõul töötavate masinate eelkäijaks tuleb lugeda harilikku kepplingu, mida kasutasid Euroopa, Aafrika ja Aasia rahvad juba kiviajal. Keppling oli tõenäoliselt ka inspiratsiooniallikaks selle masinatüübi loomisel. Põhimõtteliselt ongi ju tegemist hästi suure kepiga (heitekang), mis pöörleb endaga risti asuva telje ümber. See telg jagab ta kaheks ebavõrdse pikkusega õlaks. Pikema õla otsas on ling, millesse asetatakse heidetav kivi. Lühema õla otsas on vastukaal, mis oma raskusega alla vajudes paneb teise otsa suure kaarega läbi õhu liikuma ja selle otsa kinnitatud lingus asuv kivi saadetakse suure kiirusega teele. Blide tööpõhimõtet illustreerib joonis 9.

Vanemates seda tüüpi masinates on vastukaalu asemel köied, mida sõdalaste meeskond käskluse peale alla tõmbas. Et inimese jõud on siiski piiratud ja väga palju mehi ühe masina ümber tõmbama ei mahtunud, siis niipea kui tehnoloogiline mõte piisavalt kaugele areneda oli jõudnud, võetigi kasutusele vastukaal. Vahemärkusena tahan lisada, et tõmbajate meeskond oli ise suhteliselt suures ohus. Juhul kui kivi lingust mingil põhjusel välja ei pääsenud, oli meeskonnal suur tõenäosus sellega pihta saada.

Vaadeldava masinatüübi arengulugu algas Idamaades, kus esimesena leiutati nimetatud inimjõul töötavad masinad (joonis 10). Kas see tehnoloogia levis Euroopasse idast, või leiutati siin iseseisvalt, on siiani vaidlusalune küsimus.

Võib-olla omab siinkohal tähtsust tõik, et hiina keeles nimetatakse vastukaaluga blidet hui-hui p’ao, mis tähendab „islami kiviheitemasin”. 1271. aastal, kui taolised heitemasinad olid Euroopas juba kanda kinnitanud ja omajagu edasi arenenud, kutsus Kublai khaan spetsialiste „läänest” appi Fanchengi piiramiseks heitemasinaid ehitama. Enamik neist olevat olnud pärslased, kuid vähemalt üks ka sakslane. Igatahes on vanim inimjõul töötavat mehhanismi kujutav joonis leitud Kesk-Aasiast Samarkandi lähedalt Pendžikenti palee varemetelt seinamaali kujul. See joonis kujutab inimjõul töötavat ja lingu kasutavat blidet ning pärineb 7. sajandi lõpust või 8. sajandi algusest. Vastukaaluprintsiipi rakendava masina kohta käivad varasemad kirjalikud teated esinevad 12. sajandi keskpaiga islamimaade, Bütsantsi ja Euroopa Vahemere-äärsete piirkondade allikates. Esimene taoline joonis pärineb 12. sajandi lõpu Egiptusest (Nickel 2002: 124).

Taolised andmed näiks nagu viitavat, et hiinlased leiutasid inimeste tõmbejõul töötava masina, mida Bütsantsis, araabia-, või Vahemeremaades 12. sajandi paiku täiustati vastukaalu lisamise teel ja nii inimjõul, kui ka vastukaaluga masinad levisid sealt vastaval ajajärgul Euroopasse edasi. Kindlalt seda allikate vähesuse tõttu siiski väita ei saa.

Payne-Gallwey andmetel võtsid raskusjõul töötava blide Euroopas esmakordselt kasutusele prantslased 12. sajandil. Piiskop Egidio Colonna kirjeldanud seda kui oma aja (u. 1280. a.) kõige võimsamat heitemasinat (Payne-Gallwey 1903: 309).

Oma arengu viimastes faasides kujutas blide endast tohutult võimast relva, mis pakkus konkurentsi püssirohu jõul töötavatele suurtükkidele veel kuni kaks sajandit peale nende kasutuselevõttu. Veel aastal 1575 vaidlesid teadlased ja sõjaväelased blide või suurtüki paremuse üle. Blide eeliseks oli tema ehitamise lihtsus ja vähenõudlikkus opereerimisel. Laskemoonaks vajas ta ainult paraja suurusega kive ja õigesti opereerimiseks omajagu teadmisi. Suurtükid seevastu vajasid püssirohtu, pidevat tuleallikat ja kartsid niiskust. Viimased teated blide kasutamisest ei peegelda küll selle relva eelist suurtükkide ees, sest konkreetsetel juhtudel olid otsustavaks muud tegurid. Üks viimaseid teateid blide kasutamisest pärineb Uuest Maailmast, kus Hernan Cortés 1521. aastal Tenochtitlanit (praegune Mexico linn) piiras. Suurtükkide laskemoon oli saanud otsakorrale ja Cortés võttis vastu ettepaneku ehitada blide. See võttis mitu päeva aega ja esimene lask läks niivõrd ebaõnnestunult, et kivimürakas lendas otse üles ja alla langedes lõhkus masina (Chevedden jt 1995: 63). Kõige viimane teade blide kasutamisest sõjalisel otstarbel leidis aset lausa aastal 1779, kui inglased kasutasid seda Gibraltaril suurtükkidele kättesaamatult kuristiku põhjas peituvate hispaanlaste vastu (Hansen 1992: 191).

Blide on mänginud olulist rolli ka Eesti ajaloos. Arvatakse, et muistse vabadusvõitluse ajaks  (1208-1227) oli blide juba kõige enamlevinud heitemasina tüüp. Läti Henrik mainib oma Liivimaa kroonikas kolmel korral  ”suurt masinat”, mille omadusi kirjeldab ta üksikasjalikult Mežotne piiramisel 1219. aasta detsembris:

”Viimaks seatakse suurem masin üles, heidetakse linnusesse suuri kive, mille suurust nähes nad tunnevad linnuses suurt hirmu. Hertsog ise hakkab masina juhtijaks, heites esimese kivi, purustas nende ärkli ja mehed selle sees; ta heitis teise ja paiskas kindlustuse plangud koos palkidega maha; ta heitis kolmanda ja läbilöömisega surub kokku kindlustuse kolm suurt puud ning põrutab inimesi vigaseks. Seda nähes põgenevad linnuses olijad kindlustustest ja püüavad pääseda kindlamatesse kohtadesse; kuid et neil polnud pelgupaika, paluvad nad armu ja anuvad alla piiskopi juurde tulla” (LH XXIII, 8).

 

Raske on ette kujutada, et sellist hävitustööd võis korda saata mõni muu masin peale suuremat sorti blide. Muide, nimetatud hertsog Albert pidi järelikult masina juhtimise kunsti hästi tundma. Masina juht pidi tõenäoliselt olema masinast mõnevõrra eemal seisev inimene, kes jälgis kivi lennutrajektoori lasu ajal ja ütles, kuidas masinat järgmiseks lasuks häälestada (või tegi seda ise). Et saksi hertsog seda kunsti tundis, näitab, et tegemist oli lugupeetud ametiga.

Tõenäoliselt ehitati seesama heitemasin valmis juba 1217.-1218. aasta vahetuse paiku Saaremaa ründamiseks. Tol korral jäi masin küll kaasa võtmata, kuna talv oli äärmiselt soe, merejää ei kandnud ja Saaremaa asemel korraldati sõjakäik hoopis Läänemaale. Viimast korda mainitakse ”suurt masinat” 1227. aastal Saaremaa sõjakäiguga seoses. Seega, kui peab paika hüpotees, et tegemist on ühe ja sama masinaga (Henrik ei kõnele vahepealsel perioodil ühegi võimsa masina ehitamisest), siis kasutati ühte ja sama masinat 10 aastat järjest. Tõsi küll, sõjategevusse kaasati masin selle aja jooksul vaid kolm korda. Selline võimas heitemasin pidi olema tolle ajastu Euroopa sõjatehnika viimane sõna. Transportimisel ei veetud arvatavasti kaasa kogu masinat. Tõenäoliselt  võeti kaasa vaid heitekang, ling, päästikud ja muud keerulisemad detailid. Robustset tugistruktuuri oli lihtne ehitada ka kohapealsest materjalist (Mäesalu 2001:  88-89).

Blide ei kujutanud endast üksnes ründerelva. Henrik mainib heitemasina kasutamist ka kaitserelvana: ”Kuid neid takistavad õige suurel määral nende ammukütid, kes olid linnuses, sest neil oli linnuses õige rohkesti sõjateenistuse vendade ambe kristlaste ambude ja paterellide vastu ja nad ehitasid paterelle ja masinaid kristlaste masinate vastu, võideldes vastastikku hulga päevi.” (LH XXVII, 2) Tõenäoliselt toimus kiviheitemasinate vahel omavaheline võitlus – piirajad püüdsid tabada linnuses asuvaid masinaid ja piiratavad omakorda piirajate omi. Kuna blide heitesuuna muutmine on keeruline ja aeganõudev (selleks tuleb ju kogu masinat pöörata)[2], võis piiramise edu suures osas sõltuda heitemasina-meeskondade vahelise võistluse tulemusest – kas piirajad jõudsid enne oma masinad üles seada ja kaitsjate masinaid pommitama hakata või suutsid kaitsjad enne oma masinad vajalikku suunda pöörata, et piirajate pooleliolevad masinad purustada.

Arvamusi keskaegsete masinate võimsuse kohta on erinevaid. Blide mudelitega eksperimenteerinud Payne-Gallwey arvas, et suurimad neist olid 15 meetri pikkuse heitekangi ja umbes 9 tonnise vastukaaluga ning suutsid 140 kg kivi visata peaaegu 300 meetri kaugusele (Payne-Gallwey 1903: 309). Mõned uurijad on toonud andmeid ka märksa suuremate võimsuste kohta, näiteks sakslane Bernhard Rathgen olevat rääkinud lausa 1400 kg raskusest laskemoonast, aga kahjuks allikatele viitamata (Mäesalu 2001: 94). Sellised väited tunduvad tõepoolest uskumatuna, sest arvestades järgnevas peatükis toodud mehhaanikalist analüüsi, on taolise kivi efektiivseks heitmiseks vajalik vastukaal umbkaudu 100 tonni ringis.

3.              Vastukaaluga blide mehaanika

Käesolevas peatükis vaatlen vastukaaluga blidet kui mehaanika uurimisobjekti. Sellise käsitluse eesmärgiks on mõista blidet kui masinat füüsika seisukohast, paremini tunda tema võimeid ja piiranguid ning õppida kriitiliselt suhtuma ajalooallikatesse, aga ka mitmete humanitaarse haridusega uurijate poolt esitatud andmetesse. Samas üritan heita pilgu keskaja masinameistrite tööpõllule ja hinnata selle keerulisust. Arvestada tuleb, et keskaja meistrite käsutuses polnud arvuteid ega matemaatilisi mudeleid, vaid ainult katse-eksitus meetod ja teiste inseneride teadmised, kes tihti asusid hoopis vastase poolel.

Füüsikalises mõttes kujutab blide endast masinat, millesse vastakaalu tõstmise (vinnastamise) käigus talletatud potentsiaalne energia muutub lasu käigus heidetava keha kineetiliseks energiaks. Masina vallapäästmisel vajub vastukaal alla, tõmmates heitekangi pikema õla üles. Lingus asuv kivi lendab suure kaarega läbi õhu. Selle kaare keskpunktiks on heitekangi pikema õla ots, mis omakorda liigub kaarega läbi õhu. Heidetav kivi teeb vertikaaltasapinnas peaaegu 180° kaare ja pääseb lingust lahti masina kohal. Kivi lingust vabastamiseks on lingu üks ots kinnitatud tugevasti heitekangi külge, aga teises otsas olev rõngas libiseb mööda heitekangi tipus paiknevat konksu. Konks ja rõngas koos kindlustavad selle, et kui ling on heitekangi suhtes saavutanud teatud nurga, tuleb rõngas konksu otsast lahti ja kivi pääseb vabalt lendama.

Sõjaliselt on blide üheks olulisemaks omaduseks võimsus – võime heita suuri kive piisavalt kaugele. Esmajoones just võimsus määrab rolli, mida blide piiramise käigus võib etendada ja on tihti piiriks eduka piiramise ja ebaõnnestunud katse vahel. Muidugi mängivad oma osa ka muud omadused, nagu lasketäpsus, laskekiirus ning töökindlus. Kuid kui masin ei suuda kive linnuseni või piirajateni välja heita või suudab heita vaid niivõrd väikest laskemoona, et see vaenlasele märkimisväärset kahju ei tee, tuleb lugeda masina ehitamisse, töökorda seadmisse ja opereerimisse paigutatud vahendid raiskuläinuks.

Masina võimsus oleneb mehaanika seisukohast võttes kahest tegurist: vastukaalu massist ja vastukaalu kukkumisteekonna pikkusest (lasu jooksul läbitav kõrguste vahe). Lihtsalt ja lühidalt öeldes määravad need kaks suurust masinasse vinnastamise käigus salvestatava potentsiaalse energia hulga. Teades neid kahte suurust ning heidetava kivi massi, on lihtne arvutada kivi teoreetiliselt maksimaalne lennukaugus[3]:

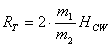                   (Siano 2001: 4)

R_T – kivi teoreetiliselt maksimaalne lennukaugus

m₁ – vastukaalu mass

m₂ – heidetava kivi mass

H_CW – vastukaalu kukkumisteekonna pikkus

 

See valem võimaldab meil hinnata allikate tõepärasust, kus esitatakse ebareaalselt suurte massidega laskemoona või pikki heitekaugusi. Lihtsamalt öeldes – masin ei saa kivi heita kaugemale, kui temasse enne viset talletatud potentsiaalne energia seda võimaldab.

Valem ise on ootuspärane. Näeme, et mida suurem on heidetava kivi mass, seda lühem on lennukaugus (pöördvõrdeline seos). Mida suuremad on vastukaalu mass ja vastukaalu kukkumisteekonna pikkus, seda pikem on kivi lennukaugus (võrdeline seos). Muud tegurid nagu masinaosade vaheline hõõrdumine, õhutakistus kivile ja masina liikuvatele osadele ning masina ebatäiuslikkus vähendavad muidugi kivi tegeliku lennukaugust. Halvasti häälestatud[4] masina puhul võib heitekaugus olla vaid 10% teoreetilisest maksimumist, tänapäevaste insenerialaste teadmiste, arvutisimulatsioonide ning kaasaegsete materjalide abil ehitatud rekonstruktsioonidel aga 70% (Jahsman 2000: 28-30).

Rusikareegel ütleb, et vastukaalu mass peaks olema umbes sada korda suurem heidetava kivi massist (Siano 2001: 40). Kui vastukaalu kukkumisteekonna pikkus oleks näiteks 2 meetrit, siis sellise masina teoreetiliselt maksimaalne heitekaugus nimetatud rusikareegli järgmise puhul on 400 meetrit. Tegelik heitekaugus, olenevalt masina häälestatusest, langeks siis vahemikku 40 – 280 meetrit.

Muidugi võib kohe lisada, et 40 meetrise heitekaugusega masin tuleks reaalse sõjategevuse seisukohalt ebaõnnestunuks lugeda.

Nimetatud kolme teguri määramisega ei tohiks tekkida märkimisväärseid probleeme. Nii kivi kui ka vastukaalu massid on lihtsasti mõõdetavad füüsikalised suurused, iseasi on muidugi ajalooallikates esitatava info täielikkus. Vahest on need suurused siiski määratavalt kaudselt.

Vastukaalu kukkumisteekonna pikkust kui küllaltki tehnilist detaili ajalooallikates kahjuks ei mainita. Masina mõõtmeid teades saab selle kohta siiski tõenäolisi hinnanguid anda või selle välja arvutada. Joonis 11 näitab, kuidas masina erinevad pikkused ja nurgad omavahel suhtuvad ning mida ja mille kaudu arvutada saab.

Näiteks kui on teada heitekangi lühema õla pikkus (tähistame selle siin l₁), siis vastukaalu kukkumisteekond (H_CW) avaldub järgmiselt:

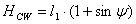            (Jahsman 2000: 30)

 

y tähistab siin nurka horisondi ja heitekangi vahel enne lasku. Enamasti on kasulik, kui see nurk on umbes 45°. Selle väärtuse võime võtta aluseks, kui allikast täpset nurka välja selgitada ei õnnestu. Oletatavate ja tõeliste väärtuste vahest tulenev heitekauguse viga ei tohiks tõenäoliselt ületada 15% (Jahsman 2000: 30).

Teoreeliselt maksimaalse ja tegeliku heitekauguse suhet nimetame masina kasuteguriks – see suurus näitab, kui suur osa masinasse enne lasku salvestatud energiast antakse kivile heite käigus üle. Nagu iga reaalse masina korral, ei saa kasutegur olla 100% ega üle selle – mingi osa energiast läheb iga füüsikalise protsessi korral kaotsi. Lisaks vähendab tegelikku heitekaugust õhutakistus kivi lennu vältel. Õhutakistuse mõju ei tohiks traditsioonilise mehaanika kaanonite järgi küll kasuteguri abil iseloomustada, kuid lihtsuse mõttes vaatame sellest praegu mööda ja loodame, et füüsikud ei pahanda.

Kasutegur on olenevalt masinast niisiis 0.1 kuni 0.7. See vahemik näib olevat väga suur, kuid alati saab teha oletusi ka masina kvaliteedi kohta. Kui masina valmistajateks on asjatundjad, võime arvata, et ka masina kasutegur on kõrge. Kui masina on valmistanud aga võhikud või masina ehituskunstiga esmakordselt kokku puutuvad ja ebapiisavalt informeeritud inimesed, peaks see peegelduma ka masina kvaliteedis ehk kasuteguris. Näiteks võib tuua tuntud juhtumi 1206. aastast, mida kirjeldab Henrik oma Liivimaa Kroonikas:

„Venelased tegid ka väikse masina sakslaste eeskujul, kuid kiviheitekunsti mitte tundes vigastasid nad väga paljusid omadest, visates kive seljataha” (LH X, 12).

Antud juhul peame kasuteguri lugema lausa negatiivseks, sest kivid lendasid nullpunktist tahapoole, seega on ka teoreetiliselt maksimaalse ja reaalse heitekauguse suhe negatiivne. Tõenäoliselt eksisid vene masinaehitajad lingu pikkuse või lingukonksu kõverusega, kuid sellel peatume juba lähemalt peatükis 3.2 . Muide, antud lõik tõestab suhteliselt ümberlükkamatult, et muistse vabadusvõitluse ajal tõid sakslased Eestisse kaasa just raskusjõul töötavad heitemasinad, sest ükski teine masinatüüp ei viska vale kasutamise korral kive selja taha.

Masina kasutegur sõltub äärmiselt paljudest teguritest ning illustreerib ilmekalt blide kui masina keerulisust ja hästihäälestatud masina ilu. Kokkuvõtlikult võime öelda, et küsimus on ajastuses. Masin tuleb seadistada nii, et kivi pääseks lingust lahti täpselt sel hetkel, kui vastukaal on lõpetanud liikumise allasuunas. Nõnda antakse võimalikult suur osa vastukaalu energiast heidetavale kivile üle. Kui kivi pääseb lahti liiga vara, läheb osa energiast raisku. Esiteks ei lenda sel juhul kivi nii kaugele kui ta võiks või ei suuda masin visata nii suurt kivi kui ta võiks. Teiseks jääb heitekang peale lasku masinasse jäänud energia tõttu pendeldama, mis on kahjulik masina konstruktsioonile (kulumine) ning pikendab aega, mille vältel ei saa alustada järgmise lasu ettevalmistamist. Heitekangi käitumine peale lasku ongi väga hea kriteerium, mille järgi saab masina kvaliteeti silma järgi hinnata, kusjuures pole vaja ei keerulisi seadmeid ega matemaatilisi mudeleid. Arvatavasti teadsid seda ka keskaegsed masinameistrid. Vastupidisel juhul, kui kivi pääseb lendu liiga hilja, siis kaotab kivi osa omale juba saadud energiast tarbetult lingu enda järel läbi õhu vedades. Tulemuseks on jällegi vähenenud heitekaugus.

Teise tingimusena peab kivi lahkumisnurk horisondi suhtes masinast pääsemise hetkel olema õige. Kui soovitakse saavutada maksimaalset heitekaugust, siis tavatingimustes on selleks nurgaks 45°. Kui aga masin ja kivi langemiskoht asuvad erinevatel kõrgustel, siis peab ka nurk olema teistsugune. Enamasti siiski ei püütud kivi heita võimalikult kaugele, vaid prooviti tabada mingit kindlat sihtmärki nagu vaenlase kindlustust või piirajate masinat, piiramistorni vms. Kindla sihtmärgi tabamiseks võimalikult suure kiviga tuli masina juhil lahendada päris keeruline ülesanne.

Järgnevalt käsitlemegi ükshaaval kõiki raskusjõul töötava heitemasina parameetreid, mida tuleb masina häälestamisel silmas pidada. Nimetatud tegurid saab laias laastus jagada kaheks: masina ehitamisel määratavad parameetrid, mida on hiljem raske või võimatu muuta ning masina kasutamise käigus muudetavad parameetrid. Muidugi saab ka masina ehitamisel määratavaid parameetreid hiljem muuta, aga see on aeganõudev ja kulukas ning näitab, et planeerimisfaasis on millegagi oluliselt eksitud.

3.1                      Masina ehitamisel määratavad tegurid

Siia jaotusesse kuuluvad kõikvõimalikud masinaosade pikkused, välja arvatud ling, mille pikkust on võimalik kergesti reguleerida masina kasutamise käigus. Muuseas, lingu reguleerimine on tegelikult väga oluline ka sihtimise seisukohast. Järgnevalt vaadeldavast kahest esimesest sõltub omakorda vastukaalu kukkumisteekonna pikkus, mis on oluliseks teguriks masina teoreetiliselt maksimaalse heitekauguse puhul.

 

Heitekangi õlgade pikkused

Heitekangi koos selle küljesoleva pöörlemisteljega, linguga ja vastukaalukorviga võib pidada kogu masina kõige tähtsamateks osadeks. Kogu ülejäänud masin kujutab endast praktiliselt ainult konstruktsiooni, mille ülesandeks on hoida heitekangi maast õigel kõrgusel. Heitekang peab olema piisavalt tugev ja võimalikult vähe painduma, sest paindes heitekang hakkab peale päästikust vabanemist vibreerima ja selle all kannatab heidete täpsus.

Heitekangi õlgade pikkuse omavaheline suhet on seni peetud üheks tähtsaimaks masinat iseloomustavaks parameetriks üldse. See määrab kiiruse, millega pöördub heitekangi lingupoolne ots, võrreldes vastukaalu langemise kiirusega. Erinevate autorite arvamused kõige õigema suhtarvu osas lähevad lahku. Näiteks P. V. Hansen kirjutab keskaegsest autorist Marinus Sanutusest, kes väitvat, et parim suhtarv on 1:5.5 või 1:6 (Hansen 1992: 200). Samas on teada, et kapten Favé ehitas keiser Napoleon III käsul masina, mille õlgade suhe oli lausa 1:33 (Hansen 1992: 193-194). Selle masina võimsus oligi märkimisväärselt madal ja põhjuseks tuleb pidada just vastukaalu poolse õla lühidust.

Õlgade pikkuste suhte määrab tegelikult piltlikult öeldes maapind. Füüsikaliselt võttes peaks vastukaalu poolne ots olema lihtsalt võimalikult pikk. See järeldub tegelikult ka eelnevalt toodud kahest valemist (vt. lk 21). Väga pikk ta ei saa olla lihtsalt sel põhjusel, et vastukaal kukuks langedes vastu maad. Jäigalt heitekangi külge kinnitatud vastukaalu puhul on reegel lihtne – vastukaalu ja maapinna vahele tuleb lihtsalt jätta teatud varu. Rippuva vastukaalu puhul aga tekib küsimus, kui pikk peaks olema vastukaalu riputusosa ehk kui kaugel heitekangist peaks vastukaal rippuma ja kui palju ruumi peaks jätma heitekangi enda jaoks. Sellel küsimusel peatun lähemalt ülejärgmises lõigus „Vastukaalu riputusosa pikkus”.

 

Telje kõrgus maast

Koos heitekangi lingupoolse õla pikkusega määrab telje kõrgus ära heitekangi algasendi ehk nurga maaga, mille all heitekang enne viske algust on. Arvutisimulatsioonid näitavad, et see on kõige kasulikum hoida umbes 45° juures. Liiga väikse nurga korral jääb vastukaalu kukkumisteekond lihtsalt väga lühikeseks, teiste sõnadega – masin pole võimeline enne viset salvestama kuigi palju energiat. Lisaks jõuab vastukaal oma trajektoori langeva osa põhja enne, kui kivi masinast lahkunud on, mille tulemusena kivi veab masinasoleku lõpuhetkedel lingu ilmaasjata läbi õhu, ilma sellelt energiat saamata. Liiga suure nurga korral ei kuku vastukaal alla aga sirgjoont pidi, vaid maa suhtes diagonaalselt. Paraja teljekõrgusega masina vastukaal kukub alla peaaegu otsejoones (vt. joonis 12). Vastukaalu diagonaalne langemistrajektoor on halb seetõttu, et osa energiast läheb vastukaalu inertsi ületamiseks, et teda horisontaalsuunas liikuma panna. Vastukaal, kui masina massiivseim osa, mis peaks soovitatavalt olema umbes 100 korda massiivsem kui heidetav kivi, omab märkimisväärset inertsi.

 

Vastukaalu riputusosa pikkus

Nüüd jõuame selleni, miks on üldse vaja vastukaal heitekangi külge kinnitada nii, et ta saaks vabalt alla rippuda. Kui vastukaal on heitekangi otsa külge jäigalt kinnitatud, siis kujutab tema trajektoor allalangemisel ringjoone kaart (vt. joonis 13). Nagu eelmises lõigus mainitud, läheb sel juhul osa energiast raisku vastukaalu inertsi ületamiseks, et teda horisontaalsuunas liikuma panna. Vabalt rippuv vastukaal langeb alla enam või vähem otsejoones ja ei kuluta energiat horisontaalsuunalisele liikumisele. Õigemini hakkab ta horisontaalsuunas liikuma siis, kui kivi on juba masinast lahkunud. Sel hetkel ongi igati hea, kui vastukaal oma inertsiga heitekangi pidurdab, et masin ei jääks pärast lasku kauaks pendeldama. See aitab vähendada masina kulumist ja lühendab aega, mis on tarvis masina järgmiseks lasuks ettevalmistamiseks. Lisaks on rippuva vastukaaluga masina massikese vinnastatud olekus madalamal ja lasu jooksul kogu struktuurile mõjuvad jõud on väiksemad, seega ei pea heitemasina tugistruktuur olema nii tugev kui jäigalt kinnitatud vastukaaluga masina puhul. Ühtlasi on  rippuvasse korvi tunduvalt mugavam vastukaalu laadida võrreldes selle kinnitamisega heitekangi külge.

Tähtis on leida, kui pikka riputusosa vastukaalu ja heitekangi vahel saab pidada optimaalseks. Riputusosa pikkus tähendab antud juhul vastukaalu massikeskme ja heitekangi poolse kinnituse vahelist vahemaad. Arvutisimulatsioonid näitavad, et mida pikem riputusosa, seda parem, sest  vastukaalu langemistrajektoor on nõnda vertikaalsem. Riputusosa pikkust piirab maapind – liiga pika riputusosa korral põrkab vastukaal langemise käigus lihtsalt vastu maad. Nagu heitekangi õlgade pikkusi käsitlevas lõigus nägime, peaks ka heitekangi lühem õlg olema võimalikult pikk. Vahemaa telje ja maapinna vahel on aga piiratud ning nii tekib küsimus - kumb neist on siis olulisem? Ühest vastust pole õnnestunud ühestki uurimusest leida. Autori enda poolt läbiviidud arvutisimulatsioonkatsetuste põhjal näis, et riputusosa pikkus peaks olema vähemalt pool heitekangi lühema õla pikkusest, et rippuva vastukaalu eelised üldse tuntavad oleksid. Sellest lühema riputusosa korral sarnaneks masin juba jäigalt kinnitatud vastukaaluga masinale. Võimalik, et optimaalne pikkus on isegi lühema õlaga võrdne või isegi pikem, see oleneb juba konkreetsest masinast. Üldkehtivat reeglit ei õnnestunud leida.

3.2                      Masina kasutamise käigus määratavad tegurid

 

Heidetava kivi mass

Arusaadavatel põhjusel on masina kasutajad läbi aegade soovinud heita võimalikult suure massiga kive. Heitemasina sõjaline efekt seisneb ju kivi poolt tekitatavates purustustes, seega mida suurem kivi, seda suuremad purustused.  Siiski tuleb arvestada, et kivi purustusjõud langemispunktis sõltub tema kineetilisest energiast, mille suurust näitab keskkoolifüüsikast tuttav valem:

 

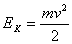
E_K – kivi kineetiline energia

m – kivi mass

v – kivi kiirus langemispunktis

 

Näeme, et kiirusest sõltub kineetiline energia isegi suuremal määral kui massist, sest kiirus on antud valemis ruudus. Seega kaugemalt visatud ja seega suurema kiirusega kergem kivi võib tekitada isegi rohkem kahju kui lähemalt visatud massiivsem kivi. Vaenlasest kaugemal asuv masin on ka vaenlase vasturünnakute eest kaitstum. Seega piirajana tuleks kindlasti eelistada vaenlasest piisavalt kaugele ehitatud masinat, mis viskab kergemaid kive ja asub väljaspool kaitsjate ambude laskeulatust.

Teiseks peegeldub siin veel üks eelis, mis oli kaitsjatel võrreldes piirajatega – kuna nende masinad asusid tavaliselt kõrgemal piirajate omadest, siis lisaks pikemale laskeulatusele oli nende poolt heidetud kividel ka suurem purustusjõud. Kaitsjate poolt heidetud kividel oli maandudes suurem kiirus, kui masinast lahkudes, piirajate omadel jällegi vastupidi.

 

Vastukaalu mass

Vastukaalu mass on põhiline masina võimsust iseloomustav tegur. Nagu varem öeldud, peaks heidetava kivi mass olema umbes üks sajandik vastukaalu massist. Võimalikud on muidugi erandid, kuid siis tuleb arvestada masina madala kasuteguriga (mis ei pruugi küll tingimata halb olla, eesmärgiks on ju siiski tabada vaenlast, mitte opereerida võimalikult efektiivse masinaga). Seos on seega väga lihtne – mida suurem vastukaal, seda võimsam masin. Teine võimsust mõjutav tegur – vastukaalu langemisteekonna pikkus – on piiratud vajadusega hoida heitekangi algnurk horisondi suhtes 45° läheduses.

 

Lingu pikkus

Õige pikkusega ling suurendab blide võimsust mitu korda. Lingu pikkus oli arvatavasti ka üks põhilisi vahendeid, mille abil kivi maandumiskohta õigele kaugusele sihiti. Pikkus tuleb valida vastavalt heidetava kivi massile – raskema kivi puhul lühem ling ja vastupidi. Kahjuks on enamiku omaaegsete jooniste peal ling kui mitte väga silmatorkav detail lihtsalt ära jäetud või siis pealiskaudselt kujutatud ning ühtegi mehhanismi lingu pikkuse reguleerimiseks pole õnnestunud tuvastada. Samas saab linguköite pikkust lihtsalt reguleerida näiteks köitesse tehtavate sõlmede abil. Ainuke tingimus seejuures on, et lingu mõlemad köied jääksid võrdse pikkusega, vastasel korral kukub kivi lingukotist lasu ajal välja.

Lingu efekt heitemasina puhul seisneb samas, mis käsilingugi puhul: heidetav keha läbib suurema kaare ja seetõttu saavutab viske käigus suurema algkiiruse. Jämedalt öeldes peaks lingu pikkus olema umbkaudu võrdne heitekangi pikema õlaga.

 

Lingu kinnituskonksu kõverus ja pikkus

Lingu kinnituskonks on see detail, mis peab garanteerima lingu avanemise ja selle kaudu kivi lahkumise masina mõju alt täpselt õigel ajahetkel. Valel ajahetkel lingust vabanev kivi lendab kas masina taha (kui vabaneb liiga vara), täpselt üles (kui vabaneb hiljem, kuid siiski liiga vara) või prantsatab otse masina ette (kui vabaneb liiga hilja).

Konksu võis valmistada kõvera või ka sirge ja lihtsalt heitekangiga teatud nurga all oleva. Konksu pikkus on kõveruse kõrval tema teine oluline parameeter. Mida pikem konks, seda hiljem ling avaneb. P. V. Hansen pakub välja omamoodi lahenduse konksu pikkuse reguleerimiseks: konksu otsa asetatakse puidust rõngaid, nii et konksu väljaulatuv osa lüheneb (vt. joonis 14). Hansen väidab, et iga selline rõngas lühendas masina heitekaugust umbes viie meetri võrra. Tegemist on seega väga täpset sihtimist võimaldava võttega (Hansen 1992: 202). Ajaloolised allikad taolistest lisanditest küll vaikivad, aga detailidest kõneldakse neis üldse üliharva.

3.3                      Laskekiirus, täpsus ja töökindlus

Masina võimsuse kõrval on tema praktilise kasutamise puhul olulised veel tema laskekiirus ehk lasuks ettevalmistamisele kuluv aeg, töökindlus ja täpsus.

Lasuks ettevalmistamise hulka kuulub masina vinnastamine, vajaduse korral ka ümberhäälestamine ja laskemoona paigutamine lingu. Peale neid tegevusi peaks masin uueks lasuks valmis olema. Laskekiirus on muidugi tugevalt sõltuv konkreetsest masinast ja võib julgelt arvata, et mida suurem masin, seda pikemaks paus kahe lasu vahel venis. Ajalooallikad jällegi palju täpset informatsiooni ei anna. Tihti on juttu vaid pidevast ja pikaajalisest pommitamisest. 1147. aastal Lissaboni piiramise ajal olevat piirajad lasknud umbes 500 kivi tunnis (Phillips 2002: 86). Siin on arvatavasti siiski mõeldud mitme masina poolt heidetud kive, sest üks lask iga 7.2 sekundi tagant ei ole usutav.

Põhiline lasuks ettevalmistamise aeg kulub masina vinnastamisele ehk heitekangi pikema õla allatõmbamisele, mille käigus heitekangi lühem õlg koos vastukaaluga tõuseb üles. Väiksemate masinate puhul saab seda teha lihtsalt mitmekesi köiest sikutades. Vastukaalu teatud massist alates muutub vinnastamine siiski inimesele ülejõukäivaks ja vaja läheb vintsi, plokke või muid taolisi abivahendeid. See suurendab vinnastamiseks kuluvat aega tunduvalt. Kui väiksema masina võib laskevalmis seada minutiga, siis suurematel võib selleks minna kuni kümme minutit.

Täpsust mõjutavad paljud tegurid. Põhiliselt kogu masina konstruktsiooni kindlus ja stabiilsus. Kui kuskilt midagi logiseb, on ka lasud ebatäpsemad. Tähis on, et heitekang ei painduks väga palju ja ei hakkaks sellest tulenevalt peale päästikust vabanemist vibreerima. Oluline on ka, et linguköis ei veniks eriti palju, see põhjustab päästikust pääsemise hetkel, kui ling koos kiviga hakkab järsu nõksatusega liikuma, kaootilist liikumist. Heitekangi pöörlemistelg ja vastukaalu riputus peavad olema kindlad. Heitekangi pöörlemistelge on hõõrdumise vähendamiseks määritud searasvaga – taolist teguviisi olevat kasutanud inglased Edward I ajal (Hansen 1992: 200). Searasv suurendab esiteks masina võimsust ja teiseks vähendab kulumist.

Töökindlus on tugevasti seotud samade teguritega, millega täpsus. Ebatäpne masin ei pea ka kaua vastu. Lisaks peab olema masin hästi häälestatud, et väga palju vastukaalu potentsiaalset energiat ei jääks peale kivi lahkumist masinasse. See väljendub heitekangi tugevas pendeldamises peale lasku. Ka laskekiirus sõltub sellest – pendeldavat masinat ei saa vinnastada, meeskond peab ootama, et masin pendeldamise lõpetaks.

3.4                      Laskemoonast

Põhiliseks laskemoonaks olid loomulikult kivid. Sihtimise seisukohast on tähtis, et kivid oleksid võimalikult sarnase massiga ning võimalikult sfäärilised. Sarnase massiga kivi puhul sai sihtimisel juhinduda eelmise kivi trajektoorist ja vastavalt vajadusele masinat ümber häälestada. Sobiva häälestuse leidmisel võis jätkata pommitamist kuni sihtmärgi purunemiseni. Ümara kivi õhutakistus on kõige väiksem, seetõttu lendasid taolised kivid kõige kaugemale. Lisaks lendasid nad ka täpsemini, kui lapikud kivid, sest lapiku kivi pöörlemine õhus võib tema trajektoori märgatavalt muuta. Pealegi sõltub lapiku kivi puhul tema lennutrajektoor sellest, kuidas ta enne lasku lingu on asetatud. Allikates esineb teateid ka laskemoonaks kasutatavate kivide tahumisest (Schmidchen 1983: 126).

Peale kivide on tähtsal kohal olnud süütelaengud. Allikates mainitakse tihti, et heitemasinatega loobiti vaenlase kindlustuste pihta „tuld” (vt. näiteks LH X, 9), kahjuks harva täpsustatakse, mis kujul. On juttu „tulepottidest või tulisest rauast” (LH XXVIII, 5). Tulepottide all  mõeldakse nähtavasti mingi süüteseguga täidetud savinõusid, millesse pistetud taht enne lasku läidetakse, ja mis sihtmärki tabades purunevad, pritsides põleva segu laiali. Hõõguma aetud raud võib olla samuti tõhus süütepomm kui ta langeb vastase puitkindlustuse või masina puitosade peale. Sellist laskemoona heitemasina ling, mis tavaliselt oli valmistatud nahast või punutud köitest, muidugi ilma eriettevalmistuseta ei talu. Hõõguvad rauatükid võidi asetada savipotti, puust või nahast ümbrisesse. Taoliste eelnevalt ettevalmistatud süütekehade eeliseks oli kindlasti nende standardsus – võisid valmistajad ju anda kehadele soovitud kuju ja massi. Seega pidi olema nendega võimalik ka täpselt lasta ja süütelaenguid paisata sinna, kus nad suurimat võimalikku kahju tegid. Võimalik, et enne süütelaengu heitmist kasutati sobiva häälestuse leidmiseks sarnase massi ja kujuga kive. See oleks analoogiline tänapäeva suurtükkide puhul kasutatavale sihtmärgi „sisselaskmisele” (vt. näiteks Peets,  Tiidolepp 1996: 58-72).

Allikates on kirjeldatud ka huvitavamat laskemoona. Psühholoogilise ja bioloogilise sõja esimesteks märkideks võime lugeda juhtumeid, kus piiratavasse linnusesse on heidetud loomaraipeid (Schmidtchen 1983: 126). Põhjuseks oli suuremalt jaolt arvatavasti psühholoogiline efekt, kuid võimalik, et ka teatud lootus kaitsjate seas haigusi levitada. Viimane võis eriti kehtida juhul kui loom oli surnud mingisse haigusse, mida loodeti kaitsjatele või nende loomadele edasi anda. Teine võimalus oli, et loodeti korjus heita kuhugi raskesti ligipääsetavasse kohta (katusele vms) kus see aja jooksul lebades lehkama ja haigusi levitama hakkas. Sellise „bioloogilise sõja” iseloomulikum näide on Kaffa piiramine mongolite poolt 1345-1346 aastatel. Piiramise ajal hävitas mongolite sõjaväge „must surm” ehk katk. Surnute kehasid visati blide abil piiratavasse linna, kust see hiljem Genua kaupmeeste laevadel Vahemere sadamatesse levis (Chevedden jt 1995: 60).

961. aastal Kreeta vallutamise puhul koostatud poeemis kirjeldab autor Theodosius, kuidas vaenlase linnusesse heideti elus eesel. Vaese looma lennutamise abil olevat tahetud näidata oma suhtumist vaenlasesse – eesleid visati eesliga. On muidugi kaheldav, et nii raske laskemoona heitmiseks vajalik masin tol ajal eksisteeris. Eriti seetõttu, et kirjeldatud on inimjõul töötavat masinat, kus vastukaalu asemel on köitest tõmbav sõjameeste meeskond. Taolised masinad jäid oma võimsuselt hilisematele vastukaaluga masinatele tunduvalt alla. Siiski näeme, et vähemalt pidi taolise laskemoona kasutamine olema usutav juba tolle aja inimesele (Dennis 1998: 106).

Eelmisega sarnaseks laskemoonaks tuleb lugeda ka vaenlase spioonide või sõjavangide kehasid. Kui piisavalt suurt masinat polnud käepärast, heideti ainult pea. Omapärasemast laskemoonast väärivad mainimist kindlasti veel väikeste kividega täidetud savipallid, mis maandumisel purunedes paiskasid oma sisu igas suunas laiali – võrreldaval kombel tänapäevaste elavjõu vastaste kartetšlaengutega. Uriini- ja fekaalitünnide mõju oli jällegi psühholoogiline, lisaeesmärgiks ebasanitaarsete tingimuste tekitamine vaenlase seas. Veel on kirjeldatud mesitarusid ning korve täis madusid ja skorpione (Hansen 1992: 203).

Viimatimainitud laskemoona puhul võib sihtimine endast kujutada märkimisväärset probleemi – suure õhutakistusega kerged kehad käituvad läbi õhu lennates ja isegi masina lingus hoopis teisiti kui kivid. Nimelt lingu liikumiskiirus võrreldes heitekangi omaga jääb väiksemaks ning sellest tulenevalt jõuab ling avanemisnurgani hiljem. Kui ling väga hilja avaneb, prantsatab laskemoon otse masina ette maha. Arvatavasti oli taoline laskemoon heitemasina meeskonnale sama ohtlik kui vaenlastele.

3.5                      Võrdlus teiste masinatüüpidega

Oleme eelnevaga lühidalt käsitlenud kõiki heitemasina olulisemaid parameetreid. Uurimata on veel vaid üks küsimus – miks ikkagi kujunes just raskusjõul töötav heitemasin keskaja kõige võimsamaks relvaliigiks. Milline on selle masinatüübi eelis teiste ees?

Suurimaks eeliseks on muidugi blide robustsus. Ta ei sisalda niiskustkartvaid köiekimpe nagu torsioonmasinad, seetõttu on relv kasutatav kõikvõimalikes ilmastikutingimustes. Tema peamiseks ehitusmaterjaliks on puit, metall ja kivid, mida võib pidada kergesti kättesaadavaks. Väga võimsa masina jaoks on vaja lihtsalt suurt vastukaalu, milleks kõlbab praktiliselt ükskõik milline suure tihedusega materjal nagu metall või kivi, vastupidiselt võimsale torsioonmasinatele, mille jõuallika valmistamiseks kulub väga palju köit. Raskusjõul töötavaid masinaid suutsid ületada alles arenenumad suurtükid, milles kasutatav püssirohi sisaldab suure ruumitihedusega keemilist energiat.

4.              Blide rekonstruktsioonid

Blide rekonstruktsioonide valmistamine ja nendega katsetamine, nagu ka muud eksperimentaalarheoloogia tegevusalad, on minevikust täielikuma arusaamise jaoks hädavajalikud. On ilmne, et taolise keerulise masina käitumist pole muul viisil võimalik täielikult mõista kui praktilise kogemuse läbi. Rekonstruktsioonidega läbiviidavad katset aitavad täiendada ühest küljest ajaloolistest allikatest pärit andmeid ning teisest küljest füüsikateaduse poolt pakutavat informatsiooni. Käesolevas peatükis püüamegi kokku võtta teadmised, mida on andnud erinevate uurijate, kaasa arvatud autori enda, poolt läbi viidud katsetused blide rekonstruktsioonidega.

Sissejuhatuses mainitud vastukaaluga heitemasinate populaarsuse kasu teaduslikule käsitlusele ei ole otsene. Selge on, et tänapäevastest materjalidest ning arvutite ja matemaatiliste mudelite abil ehitatud masinad on palju efektiivsemad keskaegsetest ametivendadest. Siiski saame me nende rekonstruktsioonide abil aimu vähemalt efektiivsuse ülemisest piirist. Lisaks on ehitatud ka omajagu ajaloolist tõepära taotlevaid rekonstruktsioone, mille tulemused on meile muidugi palju väärtuslikumad.

 

Keiser Napoleon III

Varasema perioodi üheks esimeseks eksperimendiks raskusjõul töötavate heitemasinate alal tuleb pidada 1850. aasta paiku keiser Napoleon III käsul kapten Favé poolt ehitatud masinat. Masina heitekang oli 10.3 meetrit pikk, millest lühem õlg moodustas vaid 30 cm pikkuse osa. Taoline õlgade suhe oli väga ebaõnnestunult valitud ja seda kinnitasid ka katsed. Vastukaal kaalus 4500 kg, millest 1500 kg oli jäigalt heitekangi külge kinnitatud ja 3000 kg rippus vabalt. Kahjuks pole masinast säilinud ühtegi joonist. Masinaga õnnestus sooritada neli lasku, mille tagajärjel tugistruktuur hakkas järgi andma ja katsed tuli lõpetada. Siin on nende nelja lasu tulemused:

1.             Kahurikuul kaaluga 11 kg - heitekaugus 175 m.

2.             Liivaga täidetud mürsk diameetriga 22 cm - heitekaugus 145 m.

3.             Liivaga täidetud mürsk diameetriga 27 cm - heitekaugus 120 m.

4.             Liivaga täidetud mürsk diameetriga 32 cm - heitekaugus 120 m.
(Hansen 1992: 194)

 

Rakendame eelmises peatükis käsitletud mehaanikalist käsitlust. Vastukaalu poolse õla lühiduse tõttu jääb vastukaalu langemisteekond samuti väga lühikeseks (umbes pool meetrit), mistõttu masina võimsus on väike. Nagu nägime peatükis 3, sõltub kivi teoreetiliselt maksimaalne lennukaugus otseselt heitekangi lühema õla pikkusest. Lihtne arvutus näitab, et kui vastukaalu poolne õlg oleks 2.5 meetri pikkune, suureneks masina maksimaalne heitekaugus esimeses katses kasutatud kivi korral teoreetiliselt rohkem kui kaheksa korda. See muidugi ei tähendaks kaheksa korda suuremat reaalset heitekaugust, sest õhutakistus suureneb võrdeliselt kivi algkiiruse ruuduga, kuid arvatavasti oleks masin suutnud sama kaugele paisata kaheksa korda raskema laskemoona.

 

Sir Ralph Payne-Gallwey

Varasema perioodi üheks tähtsaimaks eksperimentaatoriks tuleb kindlasti lugeda sir Ralph Payne-Gallwey’d. Oma raamatus „The Crossbow” mainib ta enda poolt ehitatud masinaid korduvalt. Suurim tema valmistatud katapult, mis oli tõenäoliselt torsioonjõul töötav masin, olevat kaalunud poolteist tonni ja heitnud kaheksanaelase kivi 450-500 jardi kaugusele. Omavalmistatud blidedel ta kahjuks lähemalt ei peatu, kuigi mainib, et on neid valmistanud mitmesuguses suuruses (Payne-Gallwey 1903: 309-315).

 

Peter Vemming Hansen

Kahekümnenda sajandi teisel poolel on rekonstruktsioone valminud niivõrd hulgaliselt, et kõigil ükshaaval me siin peatuda ei jõua. Autori jaoks on neist üheks tähtsamaks kujunenud Taani uurija ja eksperimentaatori Peter Vemming Hanseni ehitatud masinad Nykøbing Falsteri „keskaja külas”, mis kujutab endast ajaloo teemaparki ja ühtlasti uurimiskeskust.

Oma 1992. aastal ilmunud artiklis kirjeldab Hansen põhjalikku ettevalmistust, mis eelnes masina ehitusele. Meeskonda kuulusid teadusliku poole esindajatena ajaloolane, arheoloog, arhitekt ja insener. Praktilise külje eest hoolitsesid sepp, veskimeister ja taglastaja. Viimased kaks olid kaasatud nähtavasti seetõttu, et nad olid kursis „vana aja mehhanismide” ehitamisega ehk siis vastavalt veskite ja purjelaevadega. Hansen rõhutab nende isikute poolt pakutud praktiliste teadmiste kõrget väärtust. Enne lõplikku masina ehitamist valmistati mudelid skaalas 1:5 ja 1:10. Masina alus valmistati Villard de Honnecourt’i 13. sajandi keskelt pärineva visandi järgi ja ülejäänud osas lähtuti suuresti Viollet-le-Duc’i 1854. aasta joonisest. Hansen rõhutab vajadust kindlustada masina aluse horisontaalsus. Ta räägib ka ühest väga huvitavast võimalusest: nimelt ehitada masinale niiöelda topeltalus. Ülemine alus oleks masina küljes ja koos sellega oleks võimalik kogu masinat alumise aluse peal pöörata ja selle abil muuta laskesuunda. Masina üldine välimus ja laskemoonaks kasutatud betoonkuulid on näha joonis 15. Kui masinat tähelepanelikult vaadelda, võib näha, et kõige alumiste horisontaalsete prusside peal on veel teised horisontaalsed prussid, mille peale on ehitatud  masina tugistruktuur. Ta mainib samas, et masina pööramist pole veel praktikas järele proovitud. Nimelt ohutuse mõttes kinnitati masina tugistruktuur aluse külge, kuni katsete käigus on selgunud, kuidas masin käitub.

Masin ehitati niiviisi, et seda oleks võimalik taas osadeks lahti võtta ja transportida. Opereerimiseks olevat vaja 10-12 inimest, kellest kõik peale kahe on vajalikud vinnastamiseks. Vinnastamine toimub ilma vintsita, plokke läbivast köiest tõmbamise abil. Laadimisprotseduur võtab aega 5-6 minutit.

Artikli kirjutamise ajaks oli Hansen sooritanud oma masinaga 120 lasku ja peaaegu kõik nendest olid õnnestunud. Hooldust vajab see masin vähe, ainult köisi tuleb kontrollida ja heitekangi pöörlemistelge määrida. Vastukaaluks planeeriti algselt 4000 kg, kuid seni on proovitud ainult kuni 2000 kg vastukaaluga. Sealjuures saavutati betoonist valatud 15 kg sfäärilise laskemoonaga heitekauguseks 168 m. Autorile on teada, et praeguseks on samasse Nykøbing Falsteri „keskaja külasse” ehitatud veel kolm heitemasina rekonstruktsiooni, kuid andmeid nende tulemuste kohta pole kahjuks õnnestunud saada.

Tänuväärsel kombel on Hansen artiklis ära toonud ka oma heitemasina joonise. Sealt mõõdame heitekangi pikema õla pikkuseks 5.85 m ja lühema õla pikkuseks 1.2 m. See tähendab õlgade suhet 1:4.875, mis mahub kenasti üldlevinud 1:4 ja 1:5 vahemikku. Vastukaalu riputusosa pikkus on 1.35 meetrit, mis peaks olema piisav. Telje kõrgus maast on aga ainult 3.15 meetrit, mis annab heitekangi algnurgaks horisondi suhtes vaid umbes 32° soovitatava 45° asemel. Selle tõttu on vastukaalu langemisteekond ainult 1.84 meetrit 2 meetri asemel.

Nimetatud mõõtudega masina teoreetiliselt maksimaalne heitekaugus 15 kg kivi ja 2000 kg vastukaalu korral on 490 meetrit. Ülalnimetatud 168 meetrine reaalne heitekaugus annab masina kasuteguriks 0.34, mis on igati keskmine. Heitekangi telje tõstmine meetri võrra kõrgemale annaks umbes 17% võrra suurema teoreetiliselt maksimaalse heitekauguse, kui muud tegurid jääksid samaks.

 

Mati Mandel ja Jaak Mäll

Esimeseks Eestis valmistatud heitemasina rekonstruktsiooniks tuleb lugeda 1997. aastal arheoloog Mati Mandeli poolt juhitud Lihula ekspeditsiooni käigus Jaak Mälli juhtnööride järgi ehitatud masinat (joonis 16). Ain Mäesalu kohaselt on Mäll kirjutanud oma tulemustest ka artikli, mis pole kahjuks seni veel trükki jõudnud. Mäesalu kaudu saame teada ainult kahest heitetulemusest: esimesel katsel kasutati 300 kg vastukaalu ja 5 kg raskune kivi lendas umbes 40 m kaugusele. Teisel katsel kasutati 600 kg vastukaalu ja selle abil õnnestus lennutada 8 kg kaaluv kivi ligi 100 m kaugusele (Mäesalu 2005).

Heitemasinat kirjeldav artikkel Eesti Päevalehes (26.07.1997) mainib, et enne ehitama asumist valmistas Jaak Mäll kaks mudelit skaalas 1:10. Ehitusmaterjalina kasutati kuuse- ja männipalke, sepa taotud naelu ja konkse, ning kanepinööri, millega taotleti ajaloolist tõepära.

Mati Mandel koos Ain Mäesaluga ehitasid 2003. aasta suvel veel ühe heitemasina – notstali – rekonstruktsiooni, millega heideti 250 grammi kaaluv oda parimal katsel umbes 100 m kaugusele (Mäesalu 2005). Et tegemist on täiesti teist tüüpi masinaga, ei saa me siinkohal rakendada eelmises peatükis välja töötatud analüüsimetoodikat.

 

Varbola Vahvad Vennad

1999. aasta suvel valmistas Varbola Vahvate Vendade nimeline grupeering ajaloohuvilise Priidu Pärna juhtimisel Varbola linnuses kohalike puupäevade raames Lihula rekonstruktsioonist tunduvalt suurema masina (joonis 17), mis on seni suurim Eestis. Taani kuninganna järgi anti masinale nimetuseks „Helde Margarethe”. Kahjuks pole ka selle masinaga saavutatud tulemusi publitseeritud. Ehitajate endi andmeil kaalub masina vastukaal 1400 kg, heitekangi pikkus on 7.5 meetrit ja masin on võimeline heitma umbes 10 kg raskuse kivi 120 meetri kaugusele.

Kohapeal silma järgi hinnates leidis autor heitekangi õlgade suhte olevat umbkaudu 1:5.5, seega lühema õla pikkus on 1.15 m. Vastukaalu langemisteekonna pikkus on selle järgi 1.96 meetrit ja 10 kg kivi 120 meetri kaugusele heitmine annab kasuteguriks 0.22, mis on natuke vähe. Arvatavasti on madala kasuteguri põhjuseks pildilt näha olev liiga lühike ling.

 

Autori poolt läbi viidud rekonstruktsioon Otepää linnamäel

2002. aasta augustis korraldas autor Otepää linnamäel keskmise suurusega blide rekonstruktsiooni ehitamise. Keskmine on see masin tänapäeva mõistes – ta on suurem kui Lihula oma ja väiksem kui Varbola eksemplar. Omaaegsete masinate seas oleks ta arvatavasti liigitatud väiksemat tüüpi masinaks.

Töödele eelnenud planeerimisfaasis pandi paika vastukaalu mass – 500 kg, heitekangi pikkus ja õlgade suhe ning telje kõrgus maast. Muud parameetrid määratlesid ennast ise ehituse käigus. Aja- ja rahanappuse tõttu mudeleid ei ehitatud, vaid asuti kohe täissuuruses masina juurde.

Ehitustööd võtsid kokku kuus päeva, kuid täispikki tööpäevi oli nende hulgas vähe. Enamasti tuli masina ehitamisega tegeleda muude tööde kõrvalt, seetõttu on ka ehitustegevusele kokku kulunud aega väga raske hinnata. Autorit huvitas põhiliselt masina mehhaanikaline aspekt ja funktsionaalsus, ajaloolisele tõepärasusele pöörasime tähelepanu ainult niipalju, kui masina eesmärk (demonstratsioonesinemine Otepää linnusepäeva publikule) seda nõudis. Masin ehitati tervenisti kuusepalkidest, kasutades tänapäevaseid tööriistu (mootorsaed, puurid). Heitekang on 5.5 meetrit pikk, millest 1 m moodustab lühem õlg. Pöörlemistelje kõrgus maast on 3.1 m, seega moodustab heitekangi algnurk horisondi suhtes umbes 44°.

Esimene proovilask sooritati 300 kg vastukaaluga. Et masin oli üllatavalt efektiivne, siis planeeritud 500 kg vastukaaluni ei jõutudki, edasistes katsetes oli vastukaaluks 200-300 kg. Laskemoonana kasutati kive vahemikus 2-11.5 kg. Heiteid sooritati linnamäelt, mis on ümbritsevast maastikust ligikaudu 35 meetri kõrgusel. Rekonstruktsioon esindas seega niiöelda linnust kaitsvat masinat.

Parimaks tulemuseks saadi 250 kg vastukaalu ja 5 kg kivi puhul umbes 120 meetrit. Kasuteguriks saame niimoodi 0.71, kuid see on eksitav. Tuleb ju arvestada masina ja maandumispunkti kõrguste vahet. Oma trajektoori lõpupoolses otsas kukkus kivi juba kindlasti suurema kui 45° nurga all maaga, seega kui lahutame distantsist mäe kõrguse, siis saame tulemuse, millest väiksem reaalne distants tasasel maal kindlasti poleks olnud: 120 m – 35 m = 85 m. Sellise distantsi puhul saame kasuteguriks 0.5, mis on reaalne hea masina näitaja.

Proovisime ühte autori hüpoteesi – nimelt leida lahendust raskusjõul töötavate heitemasinate põlisele probleemile: küljelt-küljele sihtimisvõimaluse puudumisele. Huvi pakkus, et kas renni, milles kivi enne õhkutõusmist koos linguga lohiseb, vastukaalu poolse otsa nihutamine küljele annab mingit tulemust. Leidsime, et tulemus oli vaevumärgatav: 90 meetrise heitekauguse juures nihkus kivi maandumispunkt vaid meetri võrra küljele. See võis olla ka normaalse hajumise tulemus. Võimalik, et pikemate heitekauguste puhul oleks efekt suurem, kuid samas on ilmne, et taoline teguviis ei saa kindlasti olla lahenduseks küljelt-küljele sihtimise küsimusele.

Tõik, et raskusjõul töötav heitemasin on ülimalt stabiilne, leidis ka meie katsete käigus kinnitust. Kolm ühe ja sama kiviga sooritatud lasku lõppesid punktides, mille maksimaalne kaugus üksteisest oli kaks meetrit. Samas saime aimu isegi suhteliselt kerge (5-7 kg) kivi purustusjõust. Nimelt tungisid heidetud kivid nii sügavale maasse, et ilma raudkangi või muude abivahenditeta ei olnud võimalik neid sealt kätte saada. Oma osa mängis kindlasti ka fakt, et kivid heideti maandumiskoha suhtes 35 meetri kõrguselt, mistõttu nende kiirus maandudes oli isegi suurem kui masinast lahkumisel. Siin tuleb ilmsiks veel üks eelis, mis kaitsjatel piirajate suhtes oli – nende heidetud kivid ei lennanud mitte ainult kaugemale, vaid olid sihtpunkti jõudes ka suurema kiirusega ehk purustusjõuga.

Rekonstruktsioon õnnestus üldiselt hästi ja ka katsetest saadud kogemused olid ülimalt positiivsed. Autor võib ennast lugeda raskusjõul töötavate heitemasinate alal juba väiksemat sorti asjatundjaks ja usub, et masinaga opereerimise põhitõed on ära õpitud.

 

Peatüki lõpetuseks heidan pilgu veel tegemist vajavate tööde nimekirjale. Kindlasti tahan ka oma Otepää masinaga katseid jätkata, et uurida mitmeid küsimusi, mis seni võimaluse puudumise tõttu tähelepanuta jäid. Tahaks siinkohal nimetada erineva laskemoonaga eksperimenteerimist nagu näiteks vedelikega täidetud nõud, aga ka vastukaalu viimist planeeritud 500 kilogrammini. Samuti oleks vaja uurida seda, mis toimub trajektoori teises otsas – ehk siis kui suure reaalse purustusjõu saavutavad erineva massiga kivid.

Üldiselt tuleks rekonstruktsioonidega katsetamisel pöörata tähelepanu mitte niivõrd maksimaalse heitekauguse saavutamisele, nagu seni, vaid pigem püüda tabada kindlat sihtmärki. Vaja on välja töötada tõhus, töökindel ja kiiresti rakendatav sihtimismetoodika – lingu pikkuse ja konksu pikkuse ning kõveruse reguleerimise meetodid. Tuleks ka proovida erinevat laskemoona, sest nagu ajalooallikatest lugeda võime, kasutati blidesid mitmesuguste kehade heitmiseks, alates süütelaengutest, lõpetades mesitarudega. Tarvis on uurida nende erinevate kehade käitumist masinas ja lennu ajal.

 

5.              Kokkuvõte

Uurimistöö käigus vaatlesin heitemasinate temaatikat üldises plaanis, uurisin erinevaid heite- ja laskemasinate tüüpe ning heitsin pilgu nende ajaloolisele arengule. Leidsime, mis eristab raskusjõul töötavaid heitemasinaid teistest. Seejärel keskendusime viimatimainitud masinatüübi põhjalikule mehhaanikalisele analüüsile.

Masina rekonstruktsioone käsitlevas osas kirjeldasime lühidalt kõiki tähtsamaid töid. Peatusime ka autori poolt läbi viidud rekonstruktsioonil Otepää linnamäel. Määrasime teadaolevate andmete põhjal rekonstruktsioonide kasutegurid.

Tähtsamad järeldused, milleni raskusjõul töötava masina teoreetilise analüüsi ja praktiliste katsete põhjal jõuti, on järgmised. Olulisim kirjeldatud heitemasinat iseloomustav tegur on tema võimsus – parameeter, mis iseloomustab, kui suuri kive ja kui kaugele masin on võimeline heitma. Esitasime valemi masina teoreetiliselt maksimaalse heitekauguse arvutamiseks vastukaalu kukkumisteekonna pikkuse, vastukaalu massi ja heidetava keha massi järgi. Kivi mass ja selle heitekaugus on omavahel pöördvõrdelises seoses, vastukaalu mass ja selle kukkumisteekonna pikkus on aga võrdelises seoses heitekaugusega. Saime teada, et vastukaalu kukkumisteekonna pikkus ja selle kaudu teoreetiliselt ka maksimaalne heitekaugus on otseselt sõltuvad heitekangi lühema õla pikkusest. Lühema õla pikkust piirab maapind.

Defineerisime kasuteguri, mis kujutab endast masina teoreetiliselt maksimaalse ja tegeliku heitekauguse suhet. Leidsime, et kasutegur langeb reaalsete masinate korral vahemikku 0.1 – 0.7. Kasutegur ei näita otseselt masina kvaliteeti, sest kindla sihtmärgi tabamiseks võib masin olla meelega häälestatud mitte maksimaalsele kaugusele. Ta on pigem teoreetiline orientiir.

Leidsime, et heitekangi pendeldamine peale lasku on hea indikaator masina häälestatuse hindamiseks – hea seadistuse korral antakse kogu vastukaalu salvestatud energia heidetavale kivile edasi ja heitekang jääb peale lasku enam-vähem seisma. Halvasti häälestatud masina heitekang aga pendeldab peale lasku tugevasti, sest suur osa energiat jääb masinasse.

Kuna keskaegsete piiramiste käigus ei olnud heitemasinate eesmärgiks heita kivi võimalikult kaugele, vaid ikkagi midagi sellega tabada ja purustada, siis vaatlesime ka kivi purustusjõudu. Selle suuruse määrab ära kivi kineetiline energia maandumispunktis. Kuna kineetiline energia sõltub kivi massist esimeses astmes ja kivi kiirusest ruudus, siis järelikult on kivi kiirus purustusjõu juures massist isegi olulisem. Et kaugemale lendavad kivid lahkuvad masinast suurema algkiirusega, on nende kiirus suurem ka sihtmärki tabades. Järelikult on kasulikum visata väiksemaid kive ja kaugemalt, kui suuri kive ja lähemalt. Lisaks suuremale purustusjõule on pikem vahemaa vaenlasest ohutum ka masina meeskonnale. Antud faktis peegeldub veel üks eelis, mis oli kaitsjatel piirajate ees. Et nende heitemasinad asusid kõrgemal kui sihtmärgid, siis oli nende heidetud kividel maandudes suurem kiirus, kui masinast lahkumisel. Seetõttu omasid nad ka tunduvalt suuremat purustusjõudu kui piirajate masinatest heidetud kivid, mis maandusid heitemasinatest kõrgemal ja omasid seetõttu algkiirusest märksa väiksemat kiirust.

Antud teema uurimist ei saa kindlasti veel lõpetatuks lugeda. Nimetasime lühidalt ka tööd, mis vajaksid järgmisena tegemist. Arvukate katsetuste ja tehnilise mõtlemise abil ning ajalooallikaid üha uuesti ja uuesti läbi lugedes suudame loodetavasti taastada ammu-unustatud „kiviheitekunsti” ja selle abil mõista paremini mineviku sõdade sõlmkohti.

6.              Kasutatud allikad ja kirjandus

Allikad:

1.           LH = Henriku Liivimaa kroonika. Tõlkinud Richard Kleis, toimetanud Enn Tarvel. Tallinn, 1982.

 

Kirjandus:

 

1.           Chevedden jt. 1995 = Paul E. Chevedden, Les Eigenbrod, Vernard Foley, Werner Soedel. The Trebuchet. Scientific American, July 1995.

2.           Chevedden 2000 = Paul E. Chevedden. The Invention of the Counterweight Trebuchet: A Study in Cultural Diffusion. Dumbarton Oaks Papers, No. 54 / 2000. Washington D.C. Saadaval ka internetist: http://www.doaks.org/DOP54/DP54ch4.pdf, illustratsioonid: http://www.doaks.org/DOP54/DP54ch4pl.pdf

3.           Dennis 1998 = George T. Dennis. Byzantine Heavy Artillery: The Helepolis. Greek, Roman and Byzantine Studies 39 (1998). Saadaval ka internetist: http://www.deremilitari.org/RESOURCES/PDFs/Dennis2.pdf

4.           Hansen 1992 = Peter Vemming Hansen. Experimental Reconstruction of a Medieval Trebuchet, Acta Archaeologica vol. 63, 1992, lk. 189 - 208.

5.           Jahsman 2000 = W. E. Jahsman. The Counterweighted Trebuchet – an Excellent Example of Applied Retromechanics. http://home.att.net/~wjahsman-mta/RetroMechanics.pdf, 19.05.2005.

6.           Mäesalu 2000 = A. Mäesalu. Notstal ja springala – mõistatuslikud relvad keskaegses Eestis. - Ajalooline Ajakiri. 2000. Nr. 3. lk 5-24

7.           Mäesalu 2005 = Ain Mäesalu. Ammud, laske- ja heitemasinad muistses vabadusvõitluses ja keskaegses Eestis. (käsikiri autori valduses).

8.           Nickel 2002 = Helmut Nickel. The Mutual Influence of Europe and Asia in the Field of Arms and Armour. – Companion to Medieval Arms and Armour. The Boydell Press, 2002, lk 107-125.

9.           Payne-Gallwey 1903 = Sir Ralph Payne-Gallwey. The Crossbow. Mediæval and Modern, Military and Sporting. Its Construction History and Management. London.

10.       A. Peets, K. Tiidolepp 1996 = Ahto Peets, Kuido-Uno Tiidolepp. Suurtükiväeõpik. Eesti Riigikaitse Akadeemia. Tallinn.

11.       Phillips 2002 = Jonathan Phillips. The Crusades, 1095 – 1197. London.

12.       Schmidtchen 1983 = Volker Schmidtchen. Mittelalterliche Kriegsmaschinen. Soest.

13.       Siano 2001 = Donald B. Siano. Trebuchet Mechanics. http://www.algobeautyreb.com/trebmath35.pdf, 19.05.2005

14.       Soedel, Foley 1979 = Werner Soedel, Vernard Foley. Ancient Catapults. Scientific American, March 1979

15.       Valk 2001 = Heiki Valk. Viljandi linnuse 1223. aasta piiramisrajatised. – Viljandi Muuseumi Aastaraamat 2000. Viljandi 2001, lk 73-91.

 

Muud materjalid:

1.           Anneli Ammas. Lihulas ehitati kiviheitemasin. // Eesti Päevaleht, 26.07.1997.

2.           Piir 1996 = Ivar Piir. Füüsika ajalugu. Käsikirjaline materjal.

7.              Lisa 1: joonised

Joonis 1. Salinon'i kujuliste vastukaaludega heitemasin (Chevedden 2000, joon. 5).

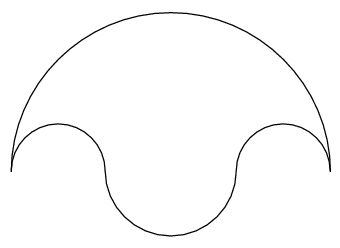
Joonis 2. Salinon ehk soolatoos.

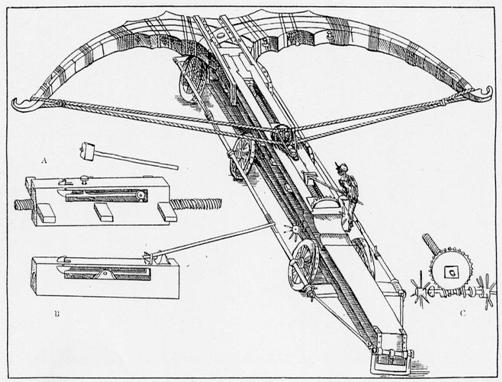
Joonis 3. Raskeamb Leonardo da Vinci kujutatuna. Arvatavasti ei ole sellist masinat päriselt kunagi ehitatud (Payne-Gallwey 1903, joon. 185).

 

Joonis 4. Raskeamb Itaalia inseneri Agostino Ramelli kujutatuna. Joonis pärineb aastast 1588 (Payne-Gallwey 1903, joon. 205)

Joonis 5. Ühekangiline heitemasin. Joonis aastast 1727 (Payne-Gallwey 1903, joon. 187).

 

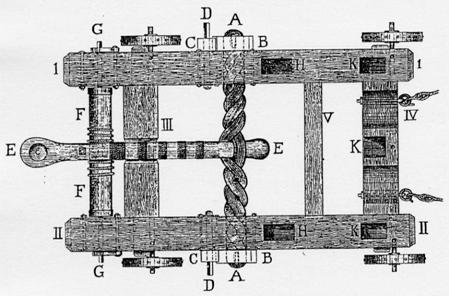
Joonis 6. Ühekangiline torsioonmasin pealtvaates (Payne-Gallwey 1903, joon. 193).

Joonis 7. Kahekangiline torsioonmasin. Joonis aastast 1607 (Payne-Gallwey 1903, joon. 186).

Joonis 8. Rooma kahekangiline torsioonmasin (Payne-Gallwey 1903, joon. 204).

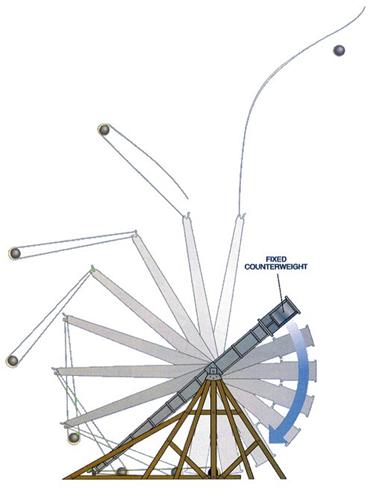
Joonis 9. Blide tööpõhimõtet selgitav joonis (Chevedden jt. 1995: 60).

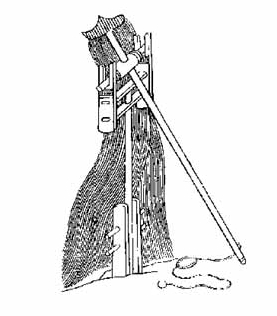
Joonis 10. Hiina blidesarnane masin (Hansen 1992, joon. 2). Vastukaalu asemel on köied, millest sõdurid korraga tõmbavad.

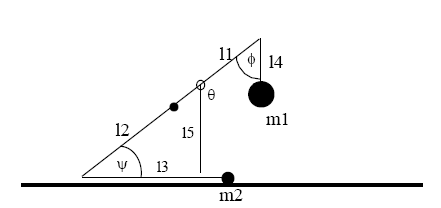
Joonis 11. Raskusjõul töötava heitemasina põhimõtteline skeem (Siano 2001, joon. 1). Masin on vinnastatud ja valmis lasuks.

Joonis 12. Vastukaalu massikeskme langemistrajektoor: vasakul väga suure teljekõrguse korral ja paremal paraja teljekõrguse korral (WinTrebStar 4.0 poolt genereeritud graafik).

Joonis 13. Vastukaalu massikeskme langemistrajektoor jäigalt kinnitatud vastukaaluga masina puhul (WinTrebStar 4.0 poolt genereeritud graafik).

Joonis 14. Lingu kinnituskonksu pikkuse reguleerimine puidust rõngaste abil (Hansen 1992, joon. 14).

Joonis 15. Peter Vemming Hanseni ehitatud esimene rekonstruktsioon Nykøbing Falsteri „keskaja külas” Taanis. Esiplaanil betoonist 15 kg raskused kuulid, mida kasutati katsetel heitemoonana (foto Nykøbing Falsteri „keskaja küla” kodulehelt www.middelaldercenteret.dk).

Joonis 16. Väikese heitemasina rekonstruktsioon Lihulas (autori foto).

Joonis 17. Varbola heitemasina vinnastamine (autori foto).

Joonis 18. Otepää heitemasin 2004 aasta sügisel. Masin on vinnastatud ja laskevalmis (autori foto).

8.              Summary: Analysis and Reconstruction of a Counterweight Trebuchet

This thesis discusses siege engines of medieval Europe, with an emphasis on counterweight trebuchets as the historically latest and technologically most advanced engine type. In addition to the role on the field of war, these machines have also played an important part in the scientific thinking of mankind. The use of counterweight trebuchets has affected the views of many historically important thinkers, from Jordanus of Nemore to Leonardo da Vinci.

All different types of engines used throughout history are presented and different typologies are discussed. A typology based on the working principle of the machine is established as the basis for this work. Then a thorough mechanical analysis of the counterweight trebuchet is presented. Each factor, like dimensions of different parts, mass of the counterweight and of the missile, sling length and axle height, is discussed separately and its contribution to the range of the machine is assessed. A formula is given to define the maximum theoretical range of a trebuchet:

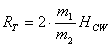
m₁ – counterweight mass

m₂ – missile mass

H_CW – height that the counterweight falls during a throw

 

If H_CW is not known, it can be assessed using the following formula:

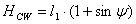
l₁ – counterweight arm length

y – angle between throwing arm and horizon at the start of the throw. If the exact value is not known, a value of 45° can be assumed.

 

As seen from these formulae, the maximum theoretical range is directly dependent on length of the counterweight arm.

Efficiency of the machine is defined as the relation of the maximum theoretical range to the real range. We find that for most machines, efficiency falls between 0.1 and 0.7.

Next we observe the most important reconstruction attempts of medieval trebuchets, including one by the author that was carried out at Otepää hill fort during the summer of 2002. Onto these reconstructed machines we apply the mechanical analysis developed previously.

Most important conclusions are the following. A good indicator of a machine’s efficiency is the swinging of the throwing arm after a throw. Violent swinging indicates bad configuration of the machine, since a lot of energy stays in the machine. A well configured machine gives most of its energy to the missile and stops after a throw almost completely. The swinging also increases wear and tear on the mechanism and does not allow starting preparations for the next throw, which is important in a siege situation.

Since in a real medieval siege it was not important to throw a stone as far as possible, but to hit a designated target instead, we analyzed the destructive power of a missile. We find that the damage done by a missile is dependent on its kinetic energy:

 

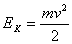
m – missile mass

v – missile velocity at collision with target

 

From this formula it can be seen, that since velocity is squared, it is much more important than mass (damage wise). Smaller missiles thrown from a longer distance (and thus arriving at a higher velocity) can do more damage than larger missiles thrown from a closer distance. Also this formula emphasizes one critical advantage that the defenders had over the besiegers: since their missiles are thrown from higher ground to lower ground, they have greater speed on impact and do more damage.

A lot of work still needs to be done in this field. Most important aspects that need experimenting and research are the behaviour of different kinds of ammunition in the machine and during the flight. Also, the events at the other end of the trajectory need to be studied: how exactly can a trebuchet be aimed, how complicated is it to hit a target and what exactly is the destructive power of a missile of a certain mass.